Вектор последовательности переходов f (s) представляет собой вектор-строку, каждая координата которой соответствует одному переходу сети Петри. Значение этой координаты определяет число срабатываний соответствующего перехода.
На рис. 2.11 приведен пример графа сети Петри, для которого будет построена матрица достижимости, а затем будет решено матричное уравнение.
t1 p2 t2
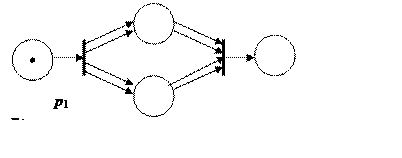 |
Рис. 2.11. Пример графа сети Петри, для которого будет построена матрица достижимости
Строками матриц D+ и D– являются переходы, а столбцами — позиции. Элементами этих матриц являются числа дуг, связывающих соответствующие позиции и переходы.
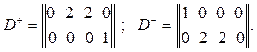
Произведем вычитание этих матриц, получим
D =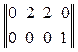 –
– 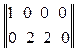 =
=
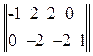 .
.
С использованием матричного уравнения решаются прямая и обратная задачи анализа сети Петри. При решении прямой задачи по известному значению исходной маркировки m и известному вектору последовательности переходов f (s) необходимо определить результирующую маркировку m1. При решении обратной задачи по известному значению результирующей маркировки m1 и установленному вектору последовательности переходов нужно определить требуемую исходную маркировку m. Таким образом, прямая задача позволяет определить будущее состояние моделируемой системы (процесса или явления) при известных исходных данных и известном законе ее функционирования. Обратная задача определяет требуемую исходную ситуацию для достижения искомой цели, если закон функционирования моделируемой системы (процесса или явления) известен. Решение данных задач сводится к решению матричного уравнения, в ходе которого производится определение неизвестных координат векторов m или m1. Если решения нет, то заданный закон функционирования системы (заданный вектор последовательности переходов) неприемлем.
Аналогично решается задача достижимости. Отличием в этом случае является то, что известными величинами являются исходная и результирующая маркировки, а требуется определить вектор последовательности переходов f (s). Рассмотрим решение такой задачи на примере сети Петри, приведенной на рис. 2.11. Определим, достижима ли маркировка μ1 = (0, 0, 0, 1) из исходной маркировки μ = (1, 0, 0, 0), то есть решим матричное уравнение
(0, 0, 0, 1) = (1, 0, 0, 0) + f (s) 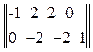 .
.
Перенесем вектор-строку (1, 0, 0, 0) в левую часть уравнения и произведем сложение векторов, получим
(-1, 0, 0, 1) =
(t1, t2)
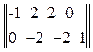 .
.
В данном уравнении неизвестные координаты вектора последовательности переходов заменены буквами. После выполнения операции умножения вектора на матрицу, получим
(-1, 0, 0, 1) = (-t1, 2t1 - 2t2, 2t1 - 2t2, t2).
Известно, что два вектора равны, когда равны соответствующие координаты этих векторов. Приравнивая координаты, получим четыре алгебраических уравнения: -t1 = –1; 2t1 -2t2 = 0; 2t1 - 2t2 = 0; t2 = 1. Решая эти уравнения, получим t1 = 1, t2 = 1, f (s) = (1, 1). Таким образом, задача достижимости имеет решение. Для получения маркировки (0, 0, 0, 1) один раз должен сработать переход t1 и один раз должен сработать переход t2. Ниже приведено дерево достижимости с корневой вершиной, равной исходной маркировке сети Петри. Данное дерево показывает, что с помощью матричного уравнения и с помощью дерева достижимости получены одинаковые решения. Это показывает, что можно выбирать любой из двух приведенных методов анализа, который более удобен для исследователя:
![]() (1, 0, 0, 0)
(1, 0, 0, 0)
t1
![]() (0, 2, 2, 0)
(0, 2, 2, 0)
t2
(0, 0, 0, 1)
Недостаток матричных уравнений в том, что вектор f
(s) определяет только
число срабатываний переходов, но он не определяет порядок этих срабатываний.
Если сеть Петри содержит петли, то они не учитываются в матрице достижимости D. Поэтому матрица достижимости не определяет однозначно
граф сети Петри и не может быть использована для анализа сетей, содержащих
петли. Ниже показаны значения двух промежуточных и итоговой матриц достижимости
для сети Петри, содержащей одну позицию и один переход, связанных между собой. D+=![]() ; D– =
; D– =![]() ; D=D+ – D–
=
; D=D+ – D–
=![]() .
.
Профессор В.НАУМОВ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.