Существуют два основных метода анализа сети, базирующихся на гра-фическом или математическом их представлении. К ним относятся метод, использующий дерево достижимости, и метод, использующий матричные уравнения. Рассмотрим эти методы.
Деревом достижимости называется ориентированный древесный граф, вершинами которого являются разметки сети — m, а дуги взвешены переходами и связывают непосредственно достижимые маркировки. На рис. 2.5 приведен граф сети Петри. Построим для данного графа дерево достижимости.
 |
Рис. 2.5. Пример графа сети Петри для построения дерева достижимости
Вектор m = (1, 0, 0, 0) задает исходную маркировку сети Петри. Она является корнем дерева достижимости. Построение дерева начинается с корня, то есть с исходной маркировки. При срабатывании перехода t1 будет получена маркировка m’ = (0, 1, 0, 0). Далее может сработать один из двух переходов: переход t2 или переход t3. При срабатывании перехода t2 будет получен вектор m’’ = (0, 0, 1, 0). Вектор m’’’ = (0, 0, 0, 1) будет получен при срабатывании перехода t3. На этом функционирование сети Петри завершится.
Построим дерево достижимости (рис. 2.6). На основе дерева достижимости можно определить и решать различные задачи анализа сети Петри. Рассмотрим примеры решения таких задач для дерева достижимости, приведенного на рис. 2.6.
1. При решении задачи достижимости маркировки m = (0, 0, 0, 0) можно сделать вывод, что такая маркировка недостижима, так как соответствующей вершины на дереве нет.
2. Решение задачи безопасности позволяет сделать вывод, что сеть безопасна, так как в каждой позиции не больше одной метки во всех возможных маркировках.
3. Результатом решения задачи сохраняемости является вывод, что сеть является строго сохраняющей. Данный вывод основан на том, что во всех вершинах дерева общее число фишек равно одной.
(1, 0, 0, 0)
¯t1
(0, 1, 0, 0)
![]() t2 t3
t2 t3
(0, 0, 1, 0) (0, 0, 0, 1)
Рис. 2.6. Пример дерева достижимости
Все задачи решаются простым перебором сети дерева достижимости в силу того, что дерево конечно.
Если множество достижимости сети Петри бесконечно, то для использования дерева нужно его представить конечным графом. В этом случае вводятся дополнительные правила для представления бесконечного процесса конечным. На рис. 2.7 приведен фрагмент бесконечного дерева достижимости для сети Петри, приведенной на этом же рисунке. Данная сеть и дерево достижимости описывают циклический процесс. Так как здесь нет правил выхода из цикла, то процесс является бесконечным.
Для исключения бесконечных циклов, а следовательно представления бесконечного дерева конечным, вводится понятие дублирующей вершины. Если на пути от корневой вершины к текущей находится маркировка, совпадающая с текущей, то текущая вершина называется дублирующей. Для такой вершины исходящих дуг на дереве достижимости нет, так как все возможные маркировки на дереве уже существуют и нет необходимости их повторять.
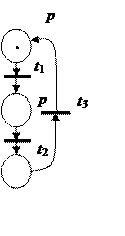 |
|||||
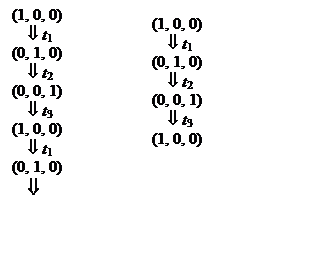 |
|||||
|
|||||
а) б) в)
Рис. 2.7. Пример бесконечного дерева достижимости: а) сеть Петри; б) фрагмент бесконечного дерева достижимости для приведенной сети Петри; в) конечное дерево достижимости
В рассматриваемом примере маркировка (1, 0, 0) определяет вершину, являющуюся дублирующей. Поэтому этой вершиной завершается построение дерева достижимости.
Если сеть не является ограниченной и сохраняющей, возможно бесконечное накопление фишек в ее позициях. Для построения конечных деревьев достижимости в этом случае вводится символ бесконечности — w. Маркировка, содержащая такой символ, называется расширенной маркировкой. Для данного символа справедливы операции сложения: w = w + n и вычитания: w = w – n, где n — конечное целое число.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.