Сети Петри. Анализ дискретных систем с помощью сетей Петри, страница 5

 

Рис. 1.15. Представление фрагмента программы сетью Петри

Сетью Петри можно описать последовательность выполнения работ, определенных сетевыми графиками. Каждой работе сетевого графика (в том числе и фиктивной работе) будет в этом случае соответствовать переход сети Петри. Это соответствует, как ранее было сказано, тому, что переход моделирует действие. На рис. 1.16 приведен пример представления сетевого графика, в котором упорядочены работы A, B, C, D, E. Работа C является фиктивной работой и представляет резерв времени, необходимый для завершения более продолжительной работы.

Если с каждым переходом связать букву алфавита некоторого языка, то сетью Петри можно задать грамматику этого языка. Последовательность срабатываний переходов образует словарь языка. На рис. 1.17 приведен простейший пример задания порождающей грамматики языка. Сеть Петри, приведенная в примере, содержит переходы, помеченные буквами грамматики (словами «сеть», «Петри»). Последовательное срабатывание двух переходов образует грамматическую конструкцию «сеть Петри».

 

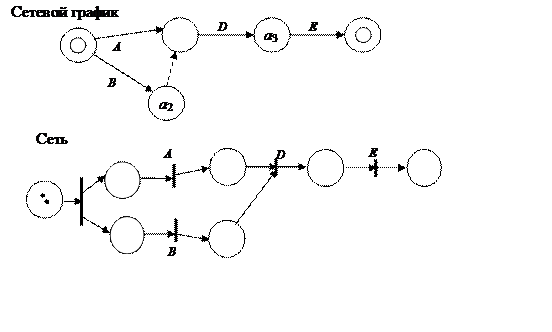
Рис. 1.16. Представление сетевого графика сетью Петри

 

Рис. 1.17. Пример сети Петри, задающей грамматику языка

2. АНАЛИЗ ДИСКРЕТННЫХ СИСТЕМ С ПОМОЩЬЮ СЕТЕЙ ПЕТРИ

2.1. Основные направления анализа

Несмотря на то, что сеть Петри — это описательная модель, она позволяет производить некоторые расчеты. На основе сетей Петри можно производить анализ свойств моделируемой системы. К задачам исследования свойств сетей Петри относятся следующие задачи.

2.1.1. Задача достижимости сети

Маркировка сети m’ называется непосредственно достижимой из маркировки m, если в нее переходит сеть при срабатывании одного перехода. Пусть, например, сеть Петри состоит из трех позиций и двух переходов. Граф сети Петри представлен на рис. 2.1.

Исходная маркировка задается вектором m = (1,0,0). При срабатывании перехода t₁ получаем маркировку m’ = (0,1,0). При срабатывании перехода t₂ получим вектор маркировки m” = (0,1,0).

 

Рис. 2.1. Граф сети Петри, состоящей из трех позиций и двух переходов

Множество маркировок сети Петри, достижимых из исходной маркировки m при срабатывании переходов, образует множество достижимости R (C,m). Для примера, приведенного на рис. 2.1:

R (С, (1, 0, 0))={(0, 1, 0); (0, 0, 1)},

где С — обозначение сети Петри; (1, 0, 0) — исходная маркировка.

Задача определения принадлежности маркировки m’ множеству достижимости R называется задачей достижимости.

2.1.2. Задача определения безопасности сети

Сеть называется безопасной, если для любой позиции р_i количество фишек в позиции не больше единицы. Для задачи безопасности должно выполняться неравенство:

m’(p_i) < 1,"p_iÎ P;

m’Î R (C, m).

Здесь каждая маркировка позиции соответствует некоторому условию. Наличие фишки в позиции обозначает выполнение этого условия, отсутствие — невыполнение.

При моделировании сетью Петри аппаратных средств, так как каждая позиция может находиться в двух состояниях (с фишкой и без фишки), позиции могут описывать функционирование триггеров.

2.1.3. Задача определения ограниченности сети

Сеть называется K-ограниченной, если для исходной маркировки m каждая позиция содержит не более K-фишек. Ограниченность сети позволяет оценить функционирование моделируемой системы в стационарном режиме, где нет бесконечного возрастания очередей. Значения K позволяют определить минимально требуемую емкость накопителей. Задачу определения ограниченности сети Петри можно формально описать следующим образом:

m’(p_i) £ K, " p_iÎ P;

m’ Î R (C, m).

Ограниченность — это обобщение свойства безопасности при K = 1. При моделировании аппаратных средств в ограниченной сети позициями можно описывать аппаратные счетчики.

2.1.4. Задача определения свойства сохраняемости

Это свойство рассматривается в случае, если с метками связаны определенные ресурсы. Свойство сохраняемости тогда трактуется как обеспечение сохраняемости этих ресурсов.