Сети Петри. Анализ дискретных систем с помощью сетей Петри, страница 6

Если оно выполняется, то при срабатывании переходов общее количество фишек в сети Петри не изменяется:

где n — число позиций в сети.

Сети, обладающие этим свойством, называются строго сохраняющими. Для них число входных и выходных позиций для каждого перехода должно быть одинаковым. На рис. 2.2 приведен пример строго сохраняющей сети, состоящей из трех позиций. В данной сети общее число фишек всегда равно единице. Фишка перемещается между позициями, что соответствует некоторому циклическому процессу. Следует отметить, что данная сеть является не только строго сохраняющей, но и безопасной.

Исходная маркировка сети m = (1, 0, 0). Ниже приведена строка, описывающая функционирование данной сети:

Множество маркировки сети имеет вид:

R(C, (1, 0, 0)) = {(1, 0, 0), (0, 1, 0), (0, 0, 1)}.

Рис. 2.2. Пример строго сохраняющей сети

В ряде случаев нет строгого взаимно-однозначного соответствия между числом фишек и количеством моделируемых ресурсов. Одной фишке может соответствовать несколько ресурсов. Тогда для обеспечения сохраняемости сети производится взвешивание этих фишек. Определяется вектор взвешивания W = (w₁, …, w_n). Чем больше ресурсов в позиции, тем больше ее вес. Сеть, для которой выполняется соотношение  называется сохраняющей. В векторной форме это можно записать Wm = Wm’, где m’Î R (C, m).

2.1.5. Задача определения активности сети

Данное свойство связано с понятием тупиков. Тупиком называется переход или переходы, которые не могут быть запущены. Свойство возможности возникновения тупиков называется свойством активности. На рис. 2.3 приведена сеть Петри. При исходной маркировке m = (0, 0) переход t₁ является тупиком.

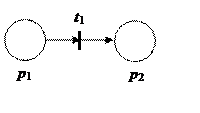Рис. 2.3. Пример сети Петри, содержащей тупик

Если исходная маркировка имеет вид m = (1, 0), то срабатывает переход t₁® m’ = (0,1). Снова возникнет тупик.

Различают разные уровни активности. Переход называется пассивным, если он не разрешен ни для какой маркировки m’ из множества достижимости R. Переход называется активным, если он не входит ни в какой тупик, то есть может срабатывать при любой маркировке из множества достижимости R.

2.1.6. Задача определения эквивалентности сетей

Кроме решения задач исследования свойств сети Петри можно решать и другие задачи. Так, например, для выбора оптимальной (рациональной) структуры системы решается задача эквивалентности нескольких альтернативных сетей Петри. При решении этой задачи можно изменить сеть Петри, не изменяя ее поведение. Изменение означает удаление пассивных переходов, которые никогда нельзя запустить, или пассивных позиций, которые никогда не могут быть маркированы, или переопределение некоторых переходов.

Две сети с одинаковым числом позиций но разным числом переходов называются эквивалентными, если они имеют одинаковые множества достижимости. Две различные маркированные сети Петри с разным числом позиций но с одинаковым числом переходов будут эквивалентными, если они будут порождать одинаковые запуски последовательностей переходов. На рис. 2.4 приведены топологически различные, однако эквивалентные сети Петри. Здесь под эквивалентностью понимается равенство множеств достижимости.

Из анализа этих двух сетей видно, что правая сеть имеет большое количество переходов и, следовательно, более сложна, чем левая. Однако, с точки зрения достижимости, эти две сети эквивалентны. Значит, эти сети задают одинаковый закон функционирования. В случае решения задач проектирования следует выбрать сеть, имеющую более простую структуру. Для рассматриваемого примера следует выбрать левую сеть:

R₁(C₁, (1, 0, 0 )) = R₂(C₂, (1,0,0)).

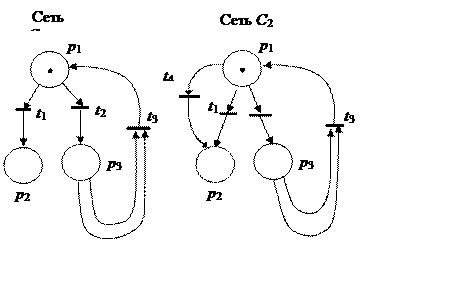Рис. 2.4. Пример эквивалентных сетей Петри

2.2. Методы анализа сетей Петри