Сети Петри. Анализ дискретных систем с помощью сетей Петри, страница 8

Если при построении дерева находятся позиции, в которых происходит накопление фишек, то значение разметки этой позиции присваивается равным w, m (р_i) = w, где p_i — позиция, в которой происходит накопление фишек.

Пусть, например, рассматривается сеть Петри, граф которой приведен на рис. 2.8. В этой сети происходит накопление фишек (заявок).

Рис. 2.8. Граф сети Петри, в которой происходит накопление фишек

Произведем маркировку данной сети. Пусть исходная маркировка описывается вектором m = (1, 0, 0). Фрагмент бесконечного дерева достижимости для такой маркировки приведен на рис. 2.9.

Ниже указан алгоритм построения конечного дерева достижимости, учитывающий как циклические процессы, так и накопление фишек. Для описания работы алгоритма введены определения вершин дерева достижимости различных типов. Все вершины дерева разделяют на граничные, внутренние, терминальные и дублирующие. Граничной называется вершина, анализируемая в текущий момент работы алгоритма. Пусть вершина х — граничная вершина.

Если для маркировки m (х) нет ни одного разрешенного перехода, то эта вершина называется терминальной. Из нее не выходит исходящих дуг. В рассматриваемом примере такой вершиной является вершина с маркировкой (0, 0, 1). Вершина, которая уже была исследована, называется внутренней.

Если вершина имеет маркировку, совпадающую с уже имеемой вершиной дерева m (y) = m (х), то она называется дублирующей. Из нее также не выходит исходящих дуг. В рассматриваемом примере такой дублирующей вершиной является, например, вершина с маркировкой (0, 1, 1).

Рис. 2.9. Фрагмент бесконечного дерева достижимости для сети Петри, приведенной на рис. 2.8

Если из вершины выходит дуга t_j, то будет порождена новая вершина z, связанная с вершиной x. Тогда возможны три ситуации:

1. Значение m (х)_i = w. Тогда для порожденной вершины z: m (z)_i = w.

2. На пути от корневой вершины к вершине х существует вершина у с меньшей маркировкой m (у) < m (х), m (у)_i < m (х)_i. В этом случае происходит порождение символа бесконечности: m (х)_i = w, m (z)_I = w. В рассматриваемом примере такой вершиной, например, является вершина с маркировкой (1, 2, 0) ® (1, w, 0).

3. Если существует разрешенная маркировка, то в порождаемой вершине z заносится эта маркировка в соответствии с правилами срабатывания перехода.

Алгоритм завершает свою работу, когда все вершины являются внутренними, терминальными, дублирующими. Дерево достижимости становится конечным.

Конечное дерево достижимости для сети Петри приведено на рис.2.10. На нем указано, к каким типам относятся все вершины дерева.

Если дерево достижимости содержит признак w, то оно не является безопасным, ограниченным и сохраняющим. Задача анализа сводится к построению конечного дерева и перебору вершин конечного дерева.

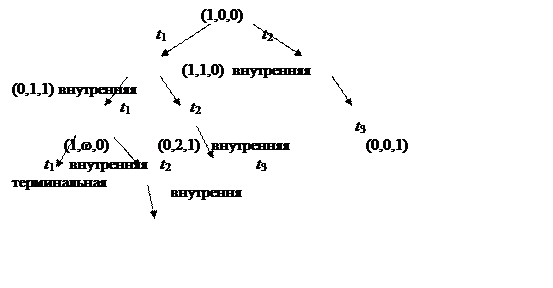Рис. 2.10. Конечное дерево достижимости для сети Петри, приведенной

 на рис.2.8

2.2.2. Матричные уравнения

Графический вариант представления функционирования сети Петри удобен при ручном решении задач анализа человеком. Если решается задача автоматизации анализа сетей Петри, то необходимо использовать методы представления графа в ЭВМ. Одним из наиболее частых методов представления графа является метод его описания с помощью матриц смежности или матриц инцидентности и затем представление матриц массивами. Матричные уравнения, применяемые для решения задач анализа, используют такое представление сети Петри.

Матричным уравнением называется уравнение вида:

,

где m — исходная маркировка сети Петри;

m¹ — результирующая маркировка;

D — матрица достижимости;

f (s) — вектор последовательности переходов.

Матрица достижимости D получается из двух промежуточных матриц: D =D⁺ – D^–, где D⁺ — выходная матрица достижимости. Данная матрица описывает выходную функцию сети Петри: D⁺[i, j] = # (p_i, O (t_j)). Матрица D^– — входная матрица достижимости. Она описывает входную функцию сети Петри: D^– [i, j] = # (p_i, I (t_j)).