 Для
повышения точности систем с программным управлением используются обратные
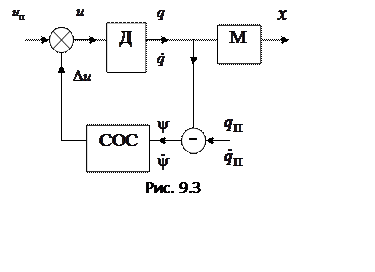
связи. Структурная схема системы с
программным управлением с обратной связью показана на рис. 9.3. Здесь на выходе
двигателя (на валу ротора) устанавливаются измерительные устройства (датчики),
измеряющие угол поворота и угловую скорость ротора и сравнивающие значения
Для
повышения точности систем с программным управлением используются обратные
связи. Структурная схема системы с
программным управлением с обратной связью показана на рис. 9.3. Здесь на выходе
двигателя (на валу ротора) устанавливаются измерительные устройства (датчики),
измеряющие угол поворота и угловую скорость ротора и сравнивающие значения ![]() и
и ![]() с их
программными значениями. Разности
с их
программными значениями. Разности ![]() и
и ![]() представляют собой ошибки по координате ротора и его угловой скорости. Сигналы
представляют собой ошибки по координате ротора и его угловой скорости. Сигналы ![]() и
и ![]() подаются на вход системы обратной связи (СОС), представляющий собой регулятор – устройство,
формирующее сигнал
подаются на вход системы обратной связи (СОС), представляющий собой регулятор – устройство,
формирующее сигнал ![]() , складывающийся с сигналом
программного управления
, складывающийся с сигналом
программного управления ![]() , подаваемым на вход
двигателя. Закон управления, связывающий сигнал обратной связи
, подаваемым на вход
двигателя. Закон управления, связывающий сигнал обратной связи ![]() с ошибками
с ошибками ![]() и
и ![]() , обычно выбирается в форме
, обычно выбирается в форме
![]() , (9.25)
, (9.25)
где ![]() и
и ![]() –
положительные коэффициенты, называемые коэффициентами усиления по координате и по скорости. Из формулы (9.25) видно, что знак корректирующего
сигнала
–
положительные коэффициенты, называемые коэффициентами усиления по координате и по скорости. Из формулы (9.25) видно, что знак корректирующего
сигнала ![]() противоположен знакам ошибок, то есть при
противоположен знакам ошибок, то есть при ![]() ,
, ![]() ,
корректирующий сигнал уменьшает величину входного параметра и тем самым
уменьшает скорость двигателя, а следовательно, и величину ошибок. При
,
корректирующий сигнал уменьшает величину входного параметра и тем самым
уменьшает скорость двигателя, а следовательно, и величину ошибок. При ![]() ,
, ![]() происходит
увеличение скорости двигателя, что также приводит к уменьшению ошибок. Таким
образом, формирование закона управления в соответствии с (9.25), вообще говоря,
направлено на уменьшение динамических ошибок, а следовательно, на повышение
точности отработки системой программного движения. Обратная связь, построенная
по такому принципу, называется отрицательной. Система, снабженная обратной связью, соединяющей ее
выход со входом, называется замкнутой.
происходит
увеличение скорости двигателя, что также приводит к уменьшению ошибок. Таким
образом, формирование закона управления в соответствии с (9.25), вообще говоря,
направлено на уменьшение динамических ошибок, а следовательно, на повышение
точности отработки системой программного движения. Обратная связь, построенная
по такому принципу, называется отрицательной. Система, снабженная обратной связью, соединяющей ее
выход со входом, называется замкнутой.
Замкнутая система,
показанная на рис. 9.3 остается работоспособной и в том случае, если сигнал ![]() на ее вход не подается. В этом случае
сигнал на входе двигателя формируется как реакция СОС на рассогласование между
законом движения
на ее вход не подается. В этом случае
сигнал на входе двигателя формируется как реакция СОС на рассогласование между
законом движения ![]() , измеренным на входе двигателя,
и программным законом
, измеренным на входе двигателя,
и программным законом ![]() , введенным на вход обратной
связи. В принципе при отсутствии ошибки (
, введенным на вход обратной
связи. В принципе при отсутствии ошибки (![]() ,
,![]() ) двигатель неподвижен, но это немедленно
приводит к появлению отрицательной ошибки, вызывающей положительный сигнал на
входе двигателя. Система, построенная по такому принципу, называется следящей.
) двигатель неподвижен, но это немедленно
приводит к появлению отрицательной ошибки, вызывающей положительный сигнал на
входе двигателя. Система, построенная по такому принципу, называется следящей.
Система, показанная
на рис. 9.3, измеряет ошибку на входе двигателя и поэтому не реагирует на
ошибки, возникающие в механической системе. В современных машинах применяются
системы, непосредственно измеряющие закон движения рабочего органа ![]() и сравнивающие его с
и сравнивающие его с ![]() . При этом сигнал
. При этом сигнал ![]() формируется
в соответствии с ошибками
формируется
в соответствии с ошибками ![]() и
и ![]() . Такие системы с обратными связями здесь
рассматриваться не будут.
. Такие системы с обратными связями здесь
рассматриваться не будут.
Вернемся к рассмотрению системы, представленной на рис. 9.1, б; предположим, что в этой системе, движение которой описывается уравнением (9.17), введена обратная связь (9.25). Подставляя в (9.17)
![]() ;
; ![]()
и предполагая, что ![]() , имеем
, имеем
![]() . (9.26)
. (9.26)
После элементарных преобразований получаем следующее уравнение для динамической ошибки:
![]() (9.27)
(9.27)
Определим динамическую ошибку при программном движении (9.13). Будем искать частное решение уравнения (9.27) в виде:
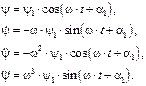 (9.28)
(9.28)
Подставим (9.28) и (9.13) в (9.27):
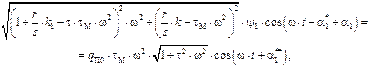 (9.29)
(9.29)
где ![]() ,
,
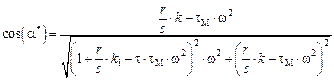 ,
,
![]() ,
,
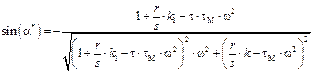 ,
,
![]() .
.
Приравняв коэффициенты при косинусах, найдем выражение для амплитуды динамической ошибки:
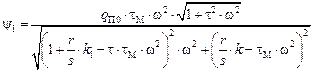 . (9.30)
. (9.30)
При отсутствии
обратной связи, то есть при ![]() ,
, ![]() , амплитуда динамической ошибки
определяется выражением
, амплитуда динамической ошибки
определяется выражением
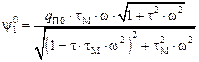 . (9.31)
. (9.31)
Эффективность введения обратной связи можно характеризовать коэффициентом эффективности, который равен отношению амплитуд ошибок в замкнутой и разомкнутой системах. Разделив (9.30) на (9.31), получаем:
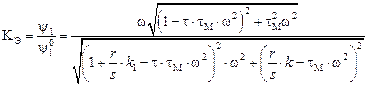 . (9.32)
. (9.32)
Чем меньше коэффициент
эффективности ![]() , тем более эффективным
оказывается введение обратной связи. Легко видеть, что первые слагаемые
подкоренных выражений в числителе и знаменателе (9.32) удовлетворяют
неравенству
, тем более эффективным
оказывается введение обратной связи. Легко видеть, что первые слагаемые
подкоренных выражений в числителе и знаменателе (9.32) удовлетворяют
неравенству
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.