Машиностроение \ Теория машин и механизмов

Ответы на экзаменационные вопросы № 36-39 дисциплины "Теория машин и механизмов" (Разбег машины с учетом динамической характеристики двигателя. Замкнутые системы управления с обратными связями), страница 3

38. Определение программного управления. Источники динамических ошибок.

При проектировании машины с программным управлением одной из главных задач является определение программного управления, обеспечивающего выполнение заданного программного движения. При этом в отличие от машин с программирующими механизмами решение кинематической задачи – задачи получения требуемого закона движения – тесно переплетается с задачей динамического анализа. С тем, как решается задача выбора программного управления, познакомимся на примере системы, схема которой приведена на рис. 9.1, б.

Составим уравнение движения механической системы

, (9.5)

где – угловое ускорение ротора двигателя, – приведенный момент инерции, – движущий момент. В связи с тем, что в системах с программным управлением возникают большие переменные инерционные силы, вызывающие значительные колебания движущего момента, при их исследовании должна использоваться динамическая характеристика двигателя. Полагаем, что используется двигатель постоянного тока с независимым возбуждением, принимаем эту характеристику в форме (8.4):

, (9.6)

где – параметры двигателя.

Пусть задан программный закон движения выходного звена . Из кинематических соотношений легко определить программный закон изменения : . (9.7)

Подставляя в (9.5), определяем закон изменения движущего момента при программном движении:

. (9.8)

Далее определяем программное управление из уравнения (9.6):

. (9.9)

Введя в рассмотрение механическую постоянную времени , приводим выражение (9.9) к форме

. (9.10)

Казалось бы, задача определения программного управления решена: подав на вход двигателя напряжение , найденное из соотношения (9.10), мы должны получить требуемый закон программного движения. В действительности, однако, имеется ряд обстоятельств, приводящих к существенным отклонениям истинного закона движения от программного, а в ряде случаев – к невозможности осуществления программного движения.

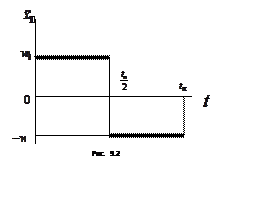Проблема реализуемости программного движения. Системы с программным управлением часто решают задачу перемещения рабочего органа из одного положения в другое при заданном законе движения. Предположим, что требуется осуществить перемещение рейки (рис. 9.1, б) на расстояние при изменении ускорения по закону, график которого показан на рис. 9.2. Здесь – время программного перемещения. Рейка должна проходить первую половину пути с постоянным ускорением . Если – величина требуемого перемещения, а начальная скорость равна нулю, то из условия равноускоренного движения имеем:

, . (9.11)

Однако осуществить такое движение невозможно. Действительно, в начальный момент ускорение должно скачком измениться от нуля до . Для этого должно скачком измениться и угловое ускорение двигателя, то есть в этот момент должно принять «бесконечно большое» значение. Но тогда бесконечно большим должно быть в начальный момент и напряжение , что, естественно, невозможно.