14. Линейное геометрическое программирование
14.1 Цель работы
Познакомиться с методами линейного программирования и получить навыки решения простейших задач путем их геометрической интерпретации с использованием вычислительной системы Mathcad.
14.2 Задание
Найти минимум целевой функции при заданных ограничениях.
|
№ |
Целевая функция |
1 ограничение |
2 ограничение |
3 ограничение |
|
1 |
2х+3у |
х+у≤5 |
х+2у≥4 |
2х+у≥5 |
|
2 |
6х+3у |
2х+у≥2 |
3х−4у≤12 |
х=2 |
|
3 |
х+2у |
х+у≤6 |
х−у≤3 |
х+у≥4 |
|
4 |
2х+4у |
х+у≤5 |
х+2у≥4 |
2х+у≥5 |
|
5 |
7х+3у |
2х+у≥2 |
3х−4у≤12 |
у=3 |
|
6 |
3х+3у |
х+у≤5 |
х+2у≥4 |
2х+у≥5 |
|
7 |
4х+3у |
х+у≤6 |
х+2у≥4 |
2х+у≥5 |
|
8 |
5х+у |
х+у≤7 |
х+2у≥4 |
у=10 |
|
9 |
6х+2у |
х+у≤8 |
х+2у≥4 |
х=5 |
|
10 |
5х+3у |
х+у≤7 |
х+2у≥4 |
2х+у≥5 |
Для всех заданий х>0, у>0.
14.3 Теоретические сведения
Линейное программирование – математический способ решения задач оптимизации, для которых целевая функция и заданные ограничения являются линейными.
Основной задачей линейного программирования является нахождение чисел x1,x2,….,xn для которых целевая функция :
 (14.1)
(14.1)
достигает наибольшего (наименьшего) значения при ограничениях
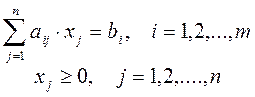 (14.2)
(14.2)
где сj,aij,bi - заданные числа.
Найденные числа x1,x2,….,xn , являющиеся решением задачи, называются оптимальным планом.
Особенностью основной задачи является то, что функциональные ограничения задаются в форме равенств. Если ограничения задаются в форме равенств и неравенств , и на некоторые ( или на все ) переменные не накладываются условие неотрицательности , то будем говорить о том , что задача представлена в общей форме. Любая задача линейного программирования может быть приведена к основной задаче.
Преобразовать неравенство в равенство можно, введя дополнительную переменную , а от условия отрицательности переменных можно заменой переменных перейти к условию неотрицательности. Область допустимых решений задачи линейного программирования представляет собой многогранник в пространстве n-переменных. В теории линейного программирования доказано, что оптимальное решение соответствует одной из вершин этого многогранника.
Решение задачи сводится к определению одной из вершин , в которой значение целевой функции меньше(больше), до тех пор, пока не будет достигнуто оптимальное значение целевой функции. Данной работе ограничимся двумя переменными, что допускает геометрическую интерпретацию решения задачи на плоскости.
Методы решения задач с большим числом переменных в данной работе не рассматриваются.
14.4 Пример выполнения задания
Рассмотрим производственную задачу. Пусть некоторая фирма изготавливает два вида красок. Цена одной тонны краски №1 равна 2 тыс. руб., а краски №2 − 3 тыс. руб. Нужно определить оптимальный суточный объем производства в тоннах для обеих красок. В качестве целевой функции выберем суммарный суточный доход фирмы :
![]()
Этот доход необходимо максимизировать.
Есть ограничения :
1) суточный спрос на краску №1 никогда не превышает спрос на краску №2 более, чем на 1 тонну х1-х2≤1,
2) суточный спрос на краску №2 никогда не превышает 2 тонны.
Для производства красок используются два вида исходных продуктов: А и В. Расход исходных продуктов для производства обоих видов красок и их возможные суточные запасы представлены в таблице 14.1.
Таблица 14.1
|
Исходный продукт |
Расход исходного продукта на 1 тонну краски |
Максимальный суточный запас, т |
|
|
Краска №1 |
Краска №2 |
||
|
А |
2 |
1 |
6 |
|
В |
1 |
2 |
8 |
Согласно таблице 14.1 можно записать ограничения на расход материалов:
для исходного продукта А : 2х1+х2≤6,
для исходного продукта В : х1+2х2≤8.
К записанным ограничениям нужно добавить естественное условие неотрицительности : х1≥0, х2≥0 .
Математическую формулировку задачи оптимизации запишем в виде:
Z=2x1+3x2 → max (14.3)
x1−x2≤1 (14.4)
2x1+x2≤6 (14.5)
x1 ≤2 (14.6)
x1+2x2≤8 (14.7)
x1≥0, x2≥0 (14.8)
Будем решать задачу в общем виде без преобразования неравенств в равенства. В связи с тем , что в задаче только две независимых переменных , она может решаться графическим методом.
Построим при помощи Mathcad многогранник ABCDEF (рис.14.1) , внутри которого находится область допустимых решений.
Оптимальное решение находится в одной из вершин этого многогранника. Нанесем на график линии уровня 1 и 2 , соответствующие различным значениям целевой функции. Увеличение значения целевой функции при движении в направлении перпендикуляра от линии 1 до линии 2.
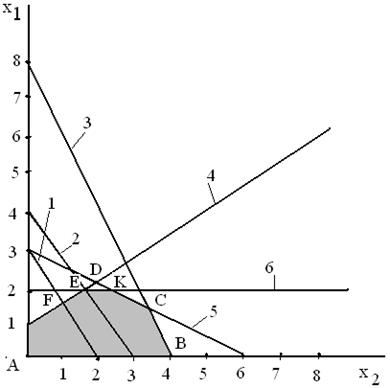
Рис.14.1
Геометрическое решение задачи (14.3) : 1− линии уровня z=6, 2 − линии уровня z=9, 3 − ограничение (14.7) по ресурсу В, 4 − ограничение (14.4), 5− ограничение (14.5) по ресурсу А , 6 − ограничение (14.6).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.