I Часть
I.1.1 Структурный анализ механизма
Целью структурного анализа механизма является определение количества звеньев и кинематических пар, классификация последних, определение подвижности пар и степени подвижности механизма, а также выделение в нем структурных групп – кинематических цепей, у которых число входов совпадает с числом степеней подвижности.
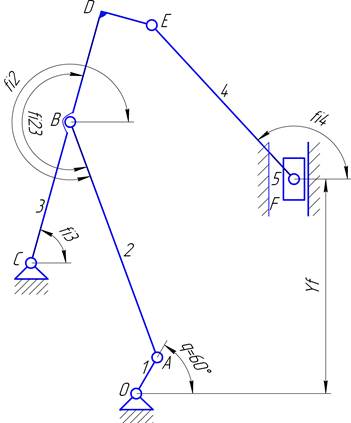
Рисунок I.1.1,1
1. ![]() (один
вход О-А).
(один
вход О-А).
2. Граф механизма:
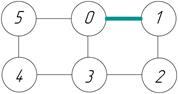
Рисунок I.1.1,1
3. Число подвижных звеньев механизма ![]() количество кинематических пар совпадает
с числом подвижностей пар
количество кинематических пар совпадает
с числом подвижностей пар ![]()
4. ![]() ,
т.е. два независимых контура
,
т.е. два независимых контура
5. ![]() (одна
степень подвижности).
(одна
степень подвижности).
6. ![]() ,
т.е. рассматривается нормальный механизм.
,
т.е. рассматривается нормальный механизм.
7. В плоскости движения нет избыточных связей и лишних подвижностей.
8. Разделение графа механизма на подграфы, соответствующие структурным группам.
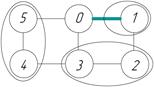
Рисунок I.1.1,2
Для открытой цепи 0-1 выполняется условие: ![]() , т.е.
, т.е. ![]() . Для замкнутых цепей 0-5-4-3-0 и 0-1-2-0
выполняется условие:
. Для замкнутых цепей 0-5-4-3-0 и 0-1-2-0
выполняется условие: ![]() .
.
9.Структурный граф механизма:
|
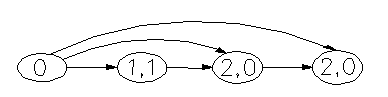
Механизм образован следующим образом: к стойке присоединяется однозвенная одноподвижная группа (звено 1) и две двухзвенные группы Ассура – ВПВ (звенья 2 и 3) и ВВП (звенья 4 и 5).
I.2.1 Геометрический анализ рычажного механизма
Целью геометрического анализа рычажного механизма является составление уравнений геометрического анализа, решение их, выделение побочных и основных решений, определяющих положения звеньев, а также исследование функций положения выходных звеньев структурных групп.
Размыкая кинематическую цепь в шарнирах А и E, приведем замкнутую цепь к открытой цепи:
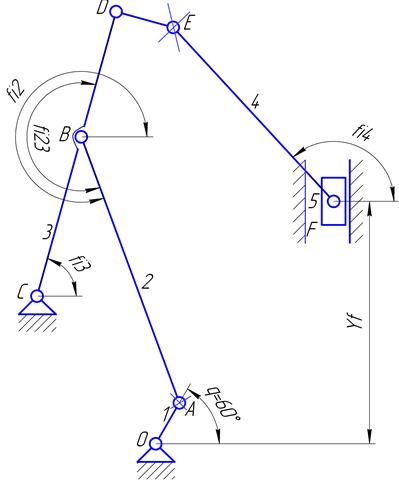
Рисунок I.2.1,4
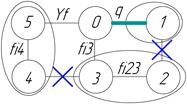
Рисунок I.2.1,5
На структурной схеме и графе механизма обозначим входную
координату ![]() и четыре
групповые координаты:
и четыре
групповые координаты: ![]() Их число совпадает с числом
разомкнутых связей:
Их число совпадает с числом
разомкнутых связей: ![]()
I.2.2 Уравнения геометрического анализа
Кривошип:
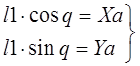
Группа ВВВ:
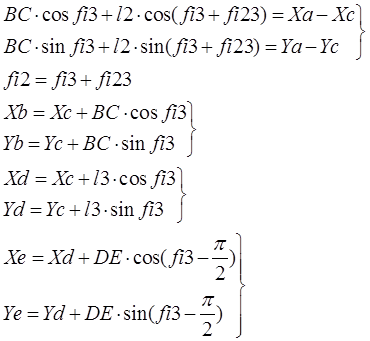
Группа ВВП:
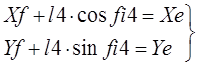
I.2.3 Решение уравнений геометрического анализа в общем виде
Решение системы уравнений для группы ВВВ:
Сгруппируем слагаемые и возведем обе части системы уравнений в квадрат, затем сложим их:
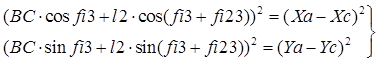
![]()
После этого получим:
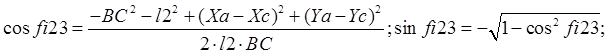
Определили относительный угол ![]() .
.
При помощи формул суммы синусов и косинусов представим систему уравнений в другом виде и сгруппируем:
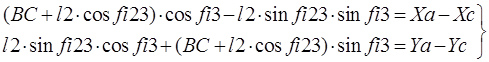
Теперь по правилу Крамера можно определить:
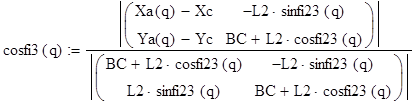
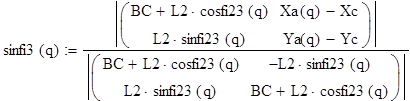
Соответственно определили относительный угол ![]() , и далее
, и далее ![]() .
.
Из системы уравнений для группы ВВП можно определить косинус
относительного угла ![]() :
:
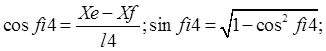
Отсюда определим относительный угол ![]() .
.
Далее определим относительную координату ![]() :
:
![]()
Найдём производные уравнений геометрического анализа по обобщённой координате q (группа ВВВ):
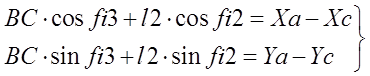
Продифференцируем первый раз:
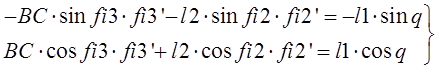
Продифференцируем второй раз:
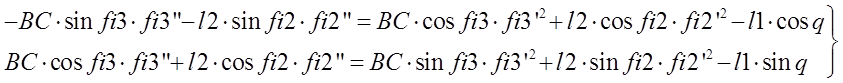
Отсюда по правилу Крамера найдем:
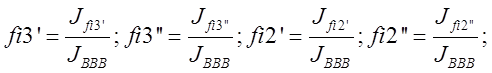
Определитель полученных систем уравнений совпадает с якобианом исходной системы уравнений группы ВВВ и выражается формулой:
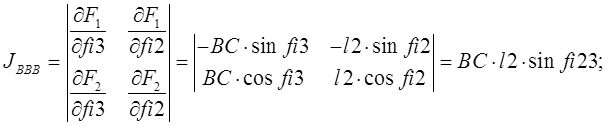
Где:
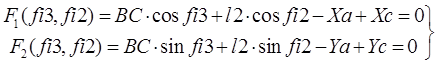
Определитель![]() получается при замене
первого столбца в определителе
получается при замене
первого столбца в определителе ![]() на столбец правых
частей уравнений:
на столбец правых
частей уравнений:
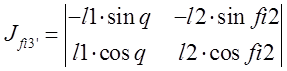
Определитель![]() получается при замене
второго столбца в определителе
получается при замене
второго столбца в определителе ![]() на столбец правых
частей уравнений:
на столбец правых
частей уравнений:
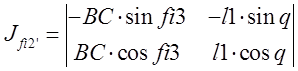
Определитель![]() получается при замене
первого столбца в определителе
получается при замене
первого столбца в определителе ![]() на столбец правых
частей уравнений:
на столбец правых
частей уравнений:
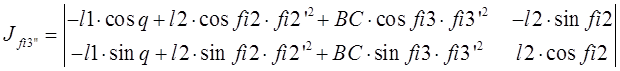
Определитель![]() получается при замене
второго столбца в определителе
получается при замене
второго столбца в определителе ![]() на столбец правых
частей уравнений:
на столбец правых
частей уравнений:
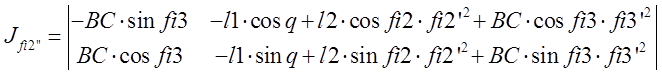
Найдём производные уравнений геометрического анализа по обобщённой координате q (группа ВВП):
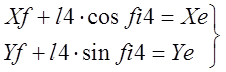
Продифференцируем первый раз:
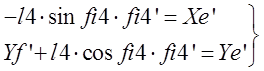
Продифференцируем второй раз:
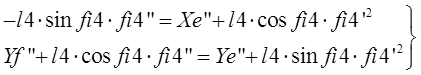
Отсюда по правилу Крамера найдем:
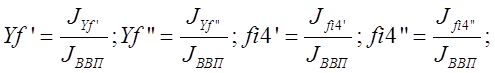
Определитель полученных систем уравнений совпадает с якобианом исходной системы уравнений группы ВВП и выражается формулой:
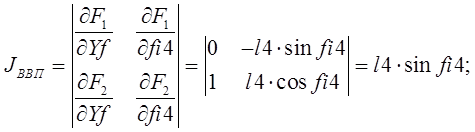
Где:
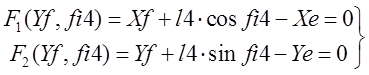
Определитель![]() получается при замене
первого столбца в определителе
получается при замене
первого столбца в определителе ![]() на столбец правых
частей уравнений:
на столбец правых
частей уравнений:
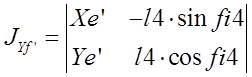
Определитель![]() получается при замене второго столбца в
определителе
получается при замене второго столбца в
определителе ![]() на столбец правых частей уравнений:
на столбец правых частей уравнений:
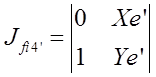
Определитель![]() получается при замене
первого столбца в определителе
получается при замене
первого столбца в определителе ![]() на столбец правых
частей уравнений:
на столбец правых
частей уравнений:
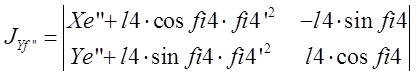
Определитель![]() получается при замене второго столбца в определителе
получается при замене второго столбца в определителе
![]() на столбец правых частей уравнений:
на столбец правых частей уравнений:
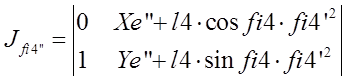
I.2.4 Построим графики функций положения ![]() и
и
![]() и их производных
и их производных
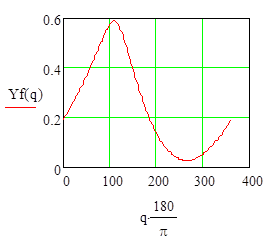
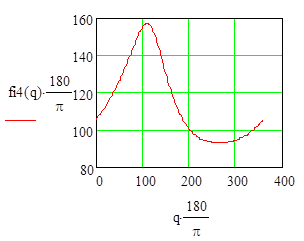
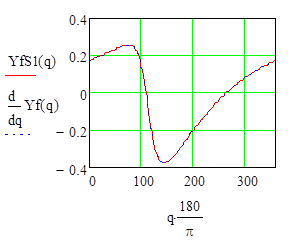
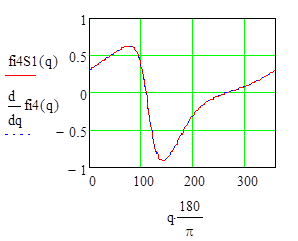
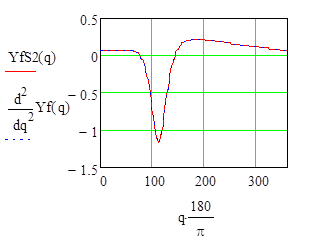
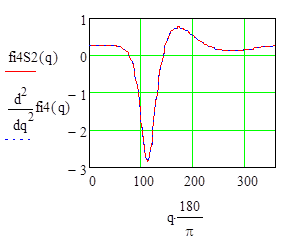
Рисунок I.2.4,6
Группа ВВВ попадает в особое положение при:
![]()
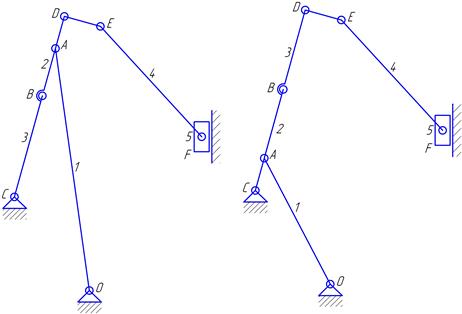
Рисунок I.2.4 ,7,1
Группа ВВП попадает в особое положение при:
![]()
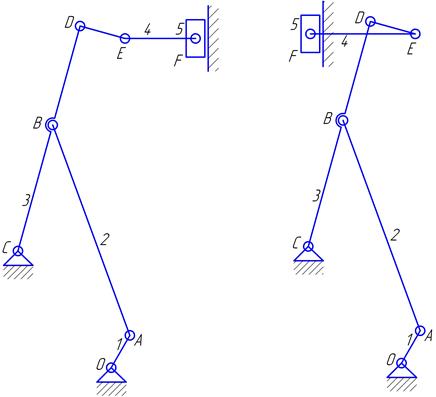
Рисунок I.2.4 ,8,2
Выберем следующие постоянные геометрические параметры кинематической схемы механизма:
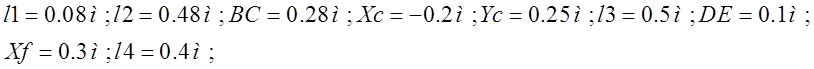
При выбранных длинах получим:
Ход: Н=0,5574м.
Kv=1,314
Изобразим механизм в крайних положениях:
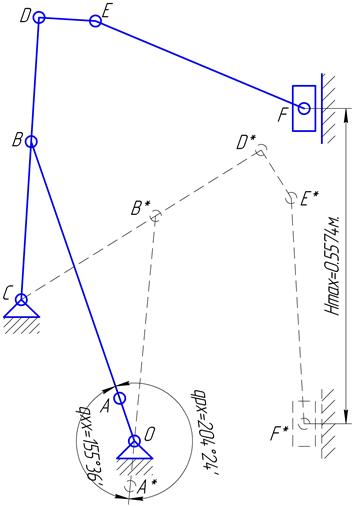
Рисунок I.2.4 ,9
12 положений механизма:
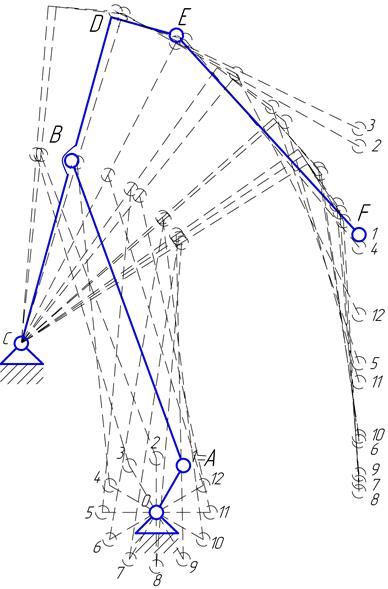
Рисунок I.2.4 ,10
I.3.1 Кинематический анализ рычажного механизма
Целью кинематического анализа является определение скоростей и ускорений отдельных точек и звеньев рычажного механизма по известному закону входного звена.
Определим в расчетном положении при ![]() скорости
и ускорения звеньев механизма и его шарнирных точек.
скорости
и ускорения звеньев механизма и его шарнирных точек.
По полученным выше формулам находим, что при ![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда при ![]() имеем:
имеем:
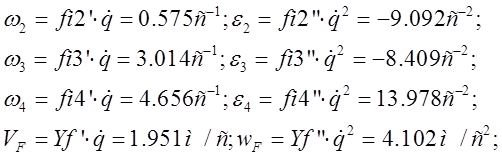
Найдем скорости и ускорения звеньев механизма и его
шарнирных точек при помощи планов скоростей и ускорений. Для этого построим
кинематическую схему механизма в расчетном положении при ![]() . С каждым подвижным звеном свяжем правую
тройку векторов
. С каждым подвижным звеном свяжем правую
тройку векторов ![]()
I.3.2 План положений
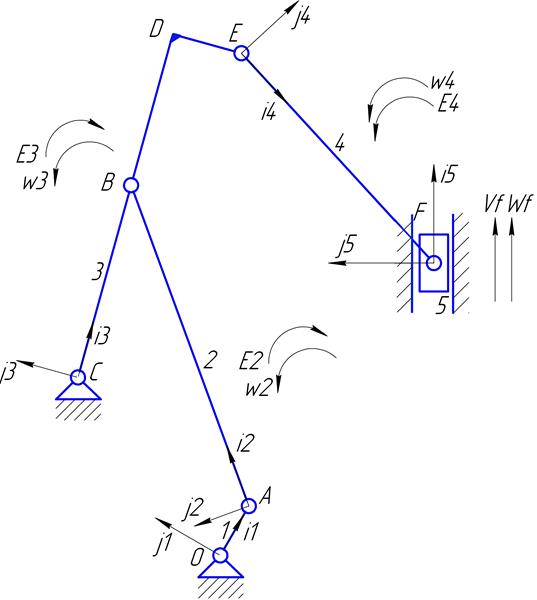
Рисунок I.3.2,11
Представим контуры ОАBCO и OEFO как сумму векторов:
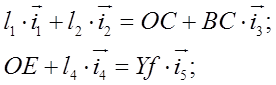
Для определения угловых и линейных скоростей продифференцируем эти равенства по времени:
Скорость точек D и E найдем из подобия.
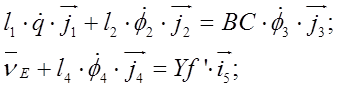
Эти уравнения можно записать в виде:
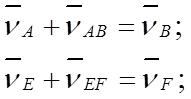
Для построения плана скоростей выберем полюс Pv и масштаб:
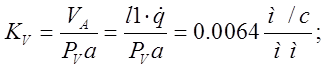
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.