12.Трение в кинематических парах. Трение скольжения, качения и верчения. Модель высшей КП с точечным контактом.
 В Кинемат.Парах
реальных механизмов возникают силы трения; часто эти силы существенно влияют на
движения механизма и должны учитываться в силовых расчетах. S –
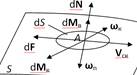
поверхность соприкосновения элементов К-ой пары. Выделим на этой поверхности
элементарную площадку dS в окрестности некоторой точки A. Рассмотрим
силы взаимодействия, возникающие на этой площадке. Главный вектор этих сил
разложим на составляющие: dN, направленную по нормали к
поверхности S, и dF, лежащую в касательной плоскости.
Главный момент относительно точки A также разложим на нормальную dMB и касательную dMk составляющие.
В Кинемат.Парах
реальных механизмов возникают силы трения; часто эти силы существенно влияют на
движения механизма и должны учитываться в силовых расчетах. S –
поверхность соприкосновения элементов К-ой пары. Выделим на этой поверхности
элементарную площадку dS в окрестности некоторой точки A. Рассмотрим
силы взаимодействия, возникающие на этой площадке. Главный вектор этих сил
разложим на составляющие: dN, направленную по нормали к
поверхности S, и dF, лежащую в касательной плоскости.
Главный момент относительно точки A также разложим на нормальную dMB и касательную dMk составляющие.
dF называется силой трения скольжения; момент dMк – моментом трения качения, момент dMв – моментом трения верчения.
Силы трения являются силами сопротивления движению =˃ dF направлена противоположно вектору относительной скорости Vск. Векторы dMк и dMв – противоположны по направлению соответственно касательной ωk и нормальной ωn составляющим вектора относительной угловой скорости.
Закон Амонтона – Кулона(закон сухого трения): ![]()
![]()
![]() где f – безразмерный коэффициент трения
скольжения, k и kв – коэффициенты трения качения и
верчения(см).
где f – безразмерный коэффициент трения
скольжения, k и kв – коэффициенты трения качения и
верчения(см).![]()
 Эти формулы
используются для определения сил трения в высш. К-ой паре с точечным
контактом. Суммарная сила трения в низшей К-ой паре:
Эти формулы
используются для определения сил трения в высш. К-ой паре с точечным
контактом. Суммарная сила трения в низшей К-ой паре:![]() где
S – поверхность соприкосновения.( Для того чтобы воспользоваться этой
формулой, нужно знать закон распределения нормальных реакций по поверхности S.)
где
S – поверхность соприкосновения.( Для того чтобы воспользоваться этой
формулой, нужно знать закон распределения нормальных реакций по поверхности S.)
Коэффициенты трения скольжения, верчения и качения определяются экспериментально; они зависят от многих факторов: от свойств материала, от чистоты обработки поверхностей.
Если скорость скольжения в точке
контакта и относительная угловая скорость =0, суммарные силы и моменты сил
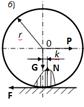
трения в К-ой паре могут быть определены из условий равновесия звеньев. N=G, F = P,
Mк = Pּr. (5.4)Нарушение состояния покоя (качение): Р≤N∙k/r (5.5)где
k – коэфф трения качения. Скольжение:
![]() ,(5.6)где fn
– коэффициент трения покоя, fn˃˃f -коэф трения скольжения.
,(5.6)где fn
– коэффициент трения покоя, fn˃˃f -коэф трения скольжения.
Модели кинематических пар с трением
 Для того, чтобы
задача силового анализа осталась разрешимой, необходимо ввести дополнительные
условия, количество которых равно числу неизвестных. Проще всего такие условия
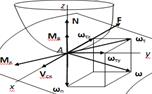
вводятся для высшей кинематической пары первого класса. Пусть поверхности
элементов пары деформируются под действием нормальной силы и касаются в малой
окрестности точки А, а относительное движение звеньев определяется
заданием скорости скольжения Vck и вектора
относительной угловой скорости ω. Направим ось z по общей нормали к
поверхностям в точке А, а ось х – по линии действия вектора Vck. Все составляющие
реакции выражаются через нормальную силу N.
Для того, чтобы
задача силового анализа осталась разрешимой, необходимо ввести дополнительные
условия, количество которых равно числу неизвестных. Проще всего такие условия
вводятся для высшей кинематической пары первого класса. Пусть поверхности
элементов пары деформируются под действием нормальной силы и касаются в малой
окрестности точки А, а относительное движение звеньев определяется
заданием скорости скольжения Vck и вектора
относительной угловой скорости ω. Направим ось z по общей нормали к
поверхностям в точке А, а ось х – по линии действия вектора Vck. Все составляющие
реакции выражаются через нормальную силу N.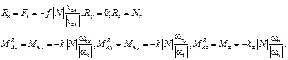
Где ωτ – компонента вектора угловой скорости, лежащая в плоскости хАy, а wtхи wty – ее проекции на оси х и y. Эти формулы выражают пять компонент реакций через шестую компоненту.
Получение аналогичных соотношений для пар с меньшей подвижностью является сложной задачей, поскольку в общем случае закон распределения нормальных реакций по поверхности или по линии соприкосновения остается неизвестным. Обычно дополнительные условия выбираются с учетом конструктивных особенностей элементов кинематической пары, позволяющих делать некоторые априорные предположения о характере распределения нормальных реакций.
13.Трение в К-их Парах.Динамические модели поступательной пары в плоском механизме с учетом трения.
Пусть при силовом расчете плоского механизма ставится задача определения реакций, лежащих в плоскости движения. При этом в идеальной поступательной паре неизвестными компонентами реакций будут (рис.5.4) сила Ry, перпендикулярная линии движения ползуна, и момент M0zR; при наличии трения возникает еще одна компонента Rx.
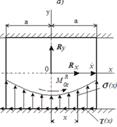 Рис. 5.4
Рис. 5.4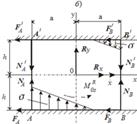
Чтобы задача силового расчета оставалась
разрешимой, эту третью компоненту необходимо выразить через первые две или
выразить все три неизвестные составляющие через какие-либо два параметра.
Сделать это можно различными способами, основываясь на разных предположениях
относительно характера распределения нормальных сил по поверхностям соприкосновения.
Предположим сначала, что эти силы распределяются некоторым образом по одной из
двух контактных плоскостей, например, по нижней (рис.5.4, а). Если s(х) –
нормальная сила, приходящаяся на единицу длины линии контакта в точке с
координатой х, то удельная сила трения t,
возникающая в той же точке, определяется из выражений (5.1) и (5.2):![]() (5.8)
Здесь функция signẋ(знак х̇) означает, что силы трения, действующие на
ползун, направлены противоположно его скорости. Из (5.8) получаем
(5.8)
Здесь функция signẋ(знак х̇) означает, что силы трения, действующие на
ползун, направлены противоположно его скорости. Из (5.8) получаем![]() (5.9)
(5.9)
поскольку в данном случае![]() Таким
образом, мы получили выражение, связывающее реакцию Rx
с Ry и тем самым сводящее число неизвестных компонент
реакций к двум. Отметим, что при соприкосновении ползуна и направляющей по
верхней плоскости знак Ryизменится
на противоположный, а знак Rx в силу (5.9) сохранится. В дальнейшем выражение (5.9)
нам будет удобно представить в форме Rx= -fRysignRy∙signẋ, с учетом того, что |Ry|=Rysign Ry
Таким
образом, мы получили выражение, связывающее реакцию Rx
с Ry и тем самым сводящее число неизвестных компонент
реакций к двум. Отметим, что при соприкосновении ползуна и направляющей по
верхней плоскости знак Ryизменится
на противоположный, а знак Rx в силу (5.9) сохранится. В дальнейшем выражение (5.9)
нам будет удобно представить в форме Rx= -fRysignRy∙signẋ, с учетом того, что |Ry|=Rysign Ry
Предположение
о том, что контакты ползуна с направляющей происходят только по одной из
плоскостей, не всегда оказывается приемлемым. Часто становится необходимым
учитывать перекос ползуна, при котором контакт возникает на обеих плоскостях
(рис.5.4, б). При этом ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.