Ответы на экзаменационные вопросы № 11-15 дисциплины "Теория машин и механизмов" (Уравнения Лагранжа 2-го рода для механизма с несколькими степенями подвижности. Трение в кинематических парах. Червячная пара), страница 3

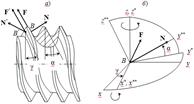
Рис.-фрагмент червяка. Рабочие поверхности витка червяка и зуба червячного колеса контактируют в точке В(В′),т.е. в зацеплении образуется пятиподвижная К-ая пара. В точке контакта возникают нормальная сила N (N′) и сила трения  F (F′), касательная к пов-ти витка червяка и направленная противоположно скорости  скольжения. Надо определить проекции этих сил на направления,|| осям червяка и червячного колеса. Введем систему координат Вхуz, где ось Вх || оси червячного колеса, ось Ву|| оси червяка, а ось Bz || линии межосевого расстояния (рис б). Если повернуть систему координат Вхуz вокруг оси Bz на угол  γ – до совмещения оси Вх с линией действия силы трения F, получим систему координат Вх*у*z*- ось Вх* будет направлена по касательной к пов-ти витка червяка в точке контакта В. Угол γ – угол подъема винтовой линии червяка (при γ = 0 винтовая линия обращается в кольцевую). Потом повернем новую систему коорд Вх*у*z* вокруг оси Вх* на угол α до совмещения оси Ву* с линией действия норм.силы N –получим новую систему корд.Вх**у** z**, в кот ось Ву** направлена ┴-но поверхности червяка  в (∙) контакта В. Угол α – угол профиля исходного контура (при α=0 виток червяка становится прямобочным).  Тогда F=-fNsign Nsignq̇ - проекции силы на оси С.коорд. Вхуz(рис 5.7)

S = Nּcosαּcosγ – Fּsinγ =N(cosαּcosγ – fּ signNּsinγּsignq̇),

P = Nּcosαּsinγ + Fּcosγ =N(cosαּsinγ + fּsignNּcosγּsignq̇),   T = Nּsinα.

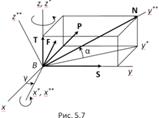S – осевая сила на червяке (окружная сила на червячном колесе); P – окружная сила на червяке (осевая на червячном колесе); Т– радиальная сила.

При изменении направления момента, приложенного к колесу, сила N также изменяет направление на противоположное, а направл силы Fменяется только при изменении знака q̇. Пусть tgψ_ч=f/cosα, где ψ_ч –приведенный угол трения червяка, тогда:

11.Уравнения Лагранжа 2-го рода для механизма с несколькими степенями подвижности.

Уравнения Лагранжа второго рода для механизма с w степенями подвижности, с жесткими звеньями и идеальными кинематическими парами могут быть получены из общего уравнения динамики. Работа сил инерции на возможном перемещении, входящая в это уравнение, может быть выражена через кинетическую энергию системы. Для механизма с w степенями подвижности справедливо: = где Т(q₁, …, q, q̇₁,…,q̇_w) – кинетическая энергия механизма, представленная как функция от обобщенных координат и их производных. В результате при независимых обобщенных координатах получаем: s = 1, … , w, где Q_s– обобщенные движущие силы;– обобщенные силы сопротивления, соответствующие всем активным силам, кроме движущих.

Кинетическая энергия каждого звена в общем случае определяется как кинетическая энергия твердого тела, совершающего сложное пространственное движение(по теореме Кенинга): , (6.20)где i – номер звена, m_i – его масса, v_ci – скорость центра масс, J_сi – тензор инерции i –го звена в его центре масс Ci, Ω_i⁽ⁱ⁾ –абсолютная угловая скорост i –го звена. Учитывая, что 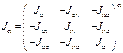, где J_x^Ci, J_y^Ci, J_z^Ci– осевые моменты инерции i-го звена, J_xy^ci, J_xz^ci, J_yz^ci –центробежные моменты инерции, а матрица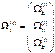,где  Ω_ix⁽ⁱ⁾, Ω_iy⁽ⁱ⁾, Ω_iz⁽ⁱ⁾ – проекции вектора угловой скорости i-го звена Ω_i  на оси i-й системы координат, выражение (6.20) запишем в виде:

Пример к 11 вопр: