Ответы на экзаменационные вопросы № 11-15 дисциплины "Теория машин и механизмов" (Уравнения Лагранжа 2-го рода для механизма с несколькими степенями подвижности. Трение в кинематических парах. Червячная пара), страница 2

В этом случае можно воспользоваться другой моделью поступательной пары. Примем условно, что нормальные силы, возникающие на поверхностях контакта, могут быть заменены двумя сосредоточенными силами N_A и N_B, приложенными в крайних точках ползуна. В зависимости от распределения нормальных сил s(х) силы N_A и N_B могут быть приложены в точках А и B , либо в точках А’ и B’ и направлены соответственно либо вверх, либо вниз. Выразим теперь все три компоненты реакций кинематической пары через два параметра – N_A и N_B. Из рис.5.4, б получаем R_y = N_A + N_B,                                             (5.11) (5.12) Учитывая, что при переходе точки контакта с одной плоскости на другую направление силы трения не изменяется, а направление момента этой силы относительно точки 0 изменяется на противоположное, получаем(5.13)

Отметим, что при отсутствии трения (f = 0) реакции N_A и N_B будут иметь разные знаки, если  Это условие, вообще говоря, может рассматриваться как критерий, указывающий на необходимость использования модели, описываемой уравнениями (5.11)-(5.13).

Для более удобного запоминания сведем модели поступательных пар в табл. 5.1.

Табл.5.1

14.Трение в К-их парах.Динамические модели вращательной пары в плоском механизме с учетом трения

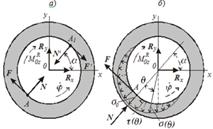
 На рис.5.5 представлены динамические модели вращательных пар с трением при учете только компонент реакций, лежащих в плоскости, перпендикулярной оси шарнира.

В модели, показанной на рис.5.5, a, предполагается, что силы нормального взаимодействия сосредоточены в точке А, и в этой же точке приложена сила трения F. Проецируя силы трения на оси координат и определяя их моменты, находимЗдесь a – угол между линией действия силы N и осью х, r – радиус цапфы. В этих формулах учтено, что с изменением знака N меняется направление силы F, поскольку точка ее приложения из А смещается в А₁.

Множитель -signφ̇ показывает, что момент сил трения, возникающих во вращательной паре, направлен противоположно относительной угловой скорости. Это выражение показывает также, что линия действия равнодействующей сил реакций во вращательной паре является касательной к окружности с радиусом  и центром в точке О.

В модели, показанной на рис.5.5, б, предполагается, что нормальные силы s(q) распределены по полуокружности симметрично относительно точки А. Обычно закон распределения выбирается в форме  Силы трения также являются распределенными; при этом τ(Ѳ)=f|s(q) |.

Проецируя силы на направление радиуса АО и перпендикулярное к нему, а также определяя момент сил относительно точки О, находим усилия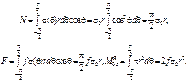т.к.|M_0z^R|=4frN/π,то           

Сравнивая эти выражения с (5.14), замечаем, что они отличаются только увеличением момента сил трения в 4/p раз. Первая модель обычно используется при расчете кинематических пар со значительными зазорами (например, изношенных).

Сведем модели вращательных пар в табл. 5.2.

15.Трение в кинематических парах.Червячная пара.