Ответы на экзаменационные вопросы № 4-24 дисциплины "Теория машин и механизмов" (Применение общего уравнения динамики для силового расчета механизмов. Разбег машины с учетом динамической характеристики двигателя)

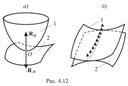
Здесь w t – угол между радиусом 0С₁ (С₁ – центр масс кулачка) и осью x, r₁= 0С₁, a – угол давления, Ф₁ и Ф₂ – силы инерции кулачка и толкателя, G₁ и G₂ – силы тяжести,  Р_пр – сила, создаваемая пружиной, прижимающей толкатель к кулачку.

б) Расчет цилиндрической зубчатой передачи. Проведем силовой анализ эвольвентной прямозубой передачи, ограничиваясь определением реакций, лежащих в плоскости движения (рис.4.15).

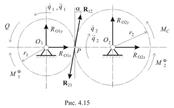Обозначим  и  – угловые скорости зубчатых колес, причем , где i – передаточное отношение; r₁ и r₂ – радиусы начальных окружностей; М_С – момент сил сопротивления; a – угол зацепления передачи, являющийся в то же время и углом давления;  и  – моменты сил инерции. Составляя уравнения кинетостатики, имеем:

– для колеса 1:

R_01x – R₂₁sina = 0; R_01y – R₂₁cosa = 0; Q – R₂₁r₁cosa  –  = 0,

– для колеса 2:

R_02x + R₁₂sina = 0; R_02y + R₁₂cosa =0; R₁₂r₂cosa  – – M_С = 0.

Решая эти уравнения, находим (учитывая, что r₂ = r₁i; ):

R_01x = R₁₂sina, R_01y = R₁₂cosa, R_02x = – R₁₂sina, R_02y = – R₁₂cosa.

6. Уравнения движения механизма в форме уравнения Лагранжа 2-го рода.  Определение приведенного момента инерции и приведенного момента сил  сопротивления  (для рычажного и зубчатого механизма).

Уравнение Лагранжа второго рода для механической системы:

 механизма, представленная как функция от обобщенной координаты и обобщенной скорости; Q – обобщенная движущая сила;

 – обобщенная сила сопротивления, соответствующие всем активным силам, кроме движущих. В механизме с одной степенью подвижности кинетическая энергия всегда может быть представлена в форме

 приведенная масса или приведенный момент инерции механизма (q- линейная или обобщенная координата). В дальнейшем будет предполагаться, что q – угловая координата, и выражение (6.3) записывается в форме

 где J(q) – приведенный момент инерции. Подставляя (6.4) в (6.1) и учитывая, что  

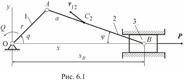
 Пример составления уравнений движения механизмов:

Для вращающегося звена 1 имеем

где J₁₀ – момент инерции звена относительно оси вращения. Для поступательно движущегося ползуна 3 получаем  Для звена 2, совершающего сложное движение, находим кинетическую энергию, пользуясь теоремой Кенига, известной из курса теоретической механики:  

относительно оси, проходящей через центр масс С₂ и перпендикулярной плоскости движения; v_C2 – скорость центра масс; w₂ – угловая скорость.

 поворота звена 2, получаем T = T₁ +T₂ +T₃ =

  

Выражение, стоящее в фигурных скобках, представляет собой приведенный момент инерции механизма J(q). Используя функции положения x_C2(q), y_C2(q), y(q), x_B(q), можно было бы представить J(q) в явной форме.J(q) – периодическая функция с периодом 2p; она представима в виде ряда:

 коэффициенты Фурье через дискретные значения периодической функции:

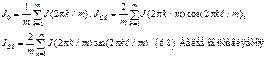 приближенное представление функций J(q) и J’(q):

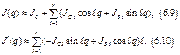
Удовлетворительная аппроксимация для l– й гармоники получается только при условии m ³ 4 l. Если силами тяжести звеньев механизма можно пренебречь,

 

Q_С часто называется приведенным моментом сил сопротивления. Функция является также периодической по q с периодом 2p.

Пример механизма с линейной функцией положения.J₁, J₂, J₃, J₄, J₅ – моменты инерции вращающихся масс относительно осей их вращения; z₁, z₂, z₃, z₄ – числа зубьев колес; M_С – момент сил сопротивления, приложенных к ротору.

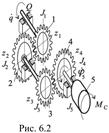
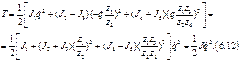
Обобщенная сила Q_С определяется в соответствии с (6.2):

 

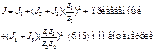
механизма. Отметим, что при приведении вращающихся масс момент инерции каждой из них делится на квадрат передаточного отношения, связывающего эту массу с входным звеном. Уравнение Лагранжа второго рода может быть использовано для определения обобщенной движущей силы Q.

8. Трение в кинематических парах. Трение скольжения, качения и верчения. Модель высшей КП с точечным контактом.

S – поверхность соприкосновения элементов кинематической пары.

Выделим на этой поверхности элементарную площадку dS  в окрестности некоторой точки A. Сила   называется силой трения скольжения; момент  – моментом трения качения, а момент  – моментом трения верчения. векторы  и  – противоположны по направлению соответственно касательной   и нормальной  составляющим вектора относительной угловой скорости. Закон Амонтона – Кулона:

     (5.1)

где f – безразмерный коэффициент трения скольжения, а k и k_В – коэффициенты трения качения и верчения.

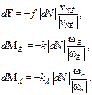(5.2)

Суммарная сила трения:  (5.3)

где S – поверхность соприкосновения. Для того чтобы воспользоваться этой формулой, нужно знать закон распределения нормальных реакций по поверхности  S.

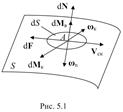Коэффициенты трения скольжения, верчения и качения определяются экспериментально; они зависят от многих факторов: от свойств материала, из которого изготовлены соприкасающиеся элементы кинематических пар, от чистоты обработки поверхностей, от наличия смазки и свойств смазочного материала, наконец, от величины относительной скорости и относительной угловой скорости звеньев. В механике машин значения этих коэффициентов предполагаются заданными и постоянными.

Формулы (5.1) и (5.2) становятся неприменимыми,если скорость скольжения в точке контакта и относительная угловая скорость равны нулю, суммарные силы и моменты сил трения в

кинематической паре могут быть определены из условий равновесия звеньев.

F = P,   M_К = Pּr. (5.4)

Нарушение состояния покоя (качение):  (5.5)

где k – коэффициент трения качения, то начнется качение цилиндра по плоскости без скольжения. Скольжение начинается при нарушении условия  , (5.6), где f_n – коэффициент трения покоя, обычно несколько превышающий величину коэффициента трения скольжения f.

Отметим попутно, что возникновение момента M_K связано с деформацией цилиндра и плоскости в зоне контакта (см. рис.5.2, б) и появлением несимметрии в распределении нормальных сил, которая