Исследование рычажного механизма, страница 2

Примечание: данный масштаб выбран для построения плана на ЭВМ в системе “Компас”.

I.3.3 План скоростей

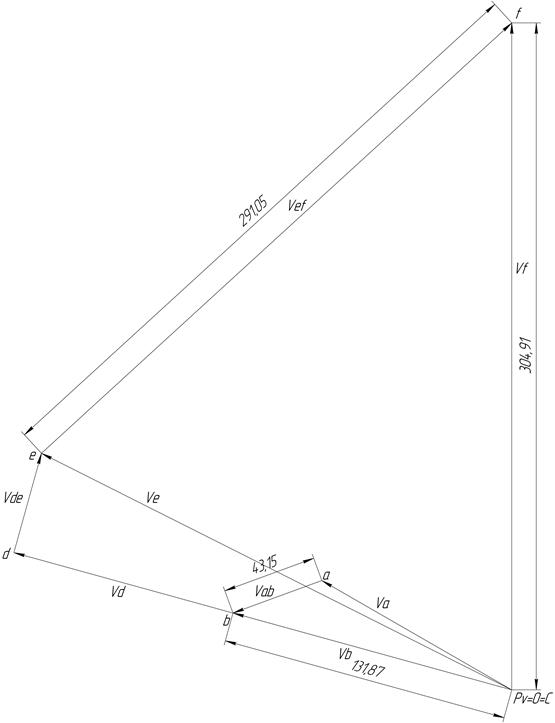
Для определения угловых и линейных ускорений продифференцируем полученные выше кинематические уравнения по времени второй раз:

Ускорение точек D и E найдем из подобия.

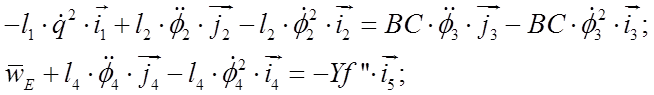
Эти уравнения можно записать в виде:

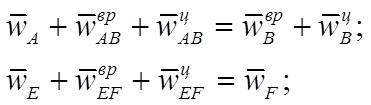
Для построения плана ускорений выберем полюс Рw и масштаб:

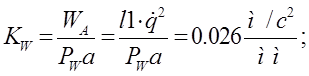
Примечание: данный масштаб выбран для построения плана на ЭВМ в системе “Компас”.

I.3.4 План ускорений

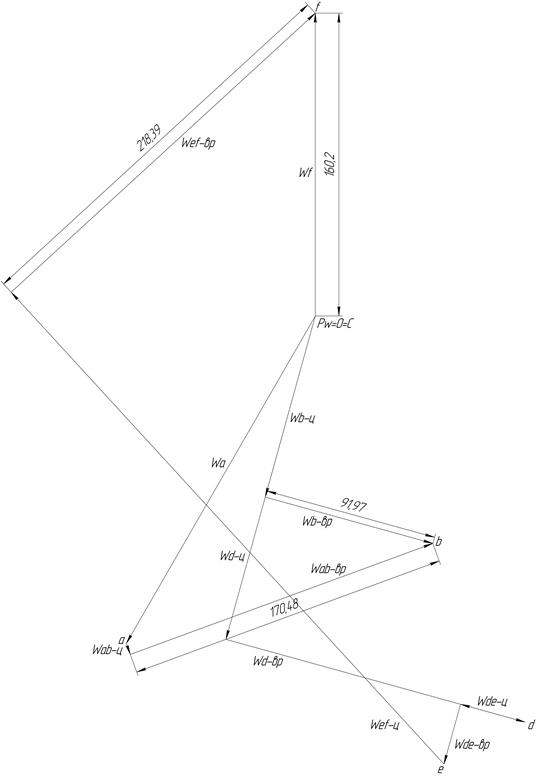
Сравним кинематические параметры механизма, полученные аналитическим и графоаналитическим методами.

I.3.7 Таблица сравнений №1

	Аналитический метод	Графоаналитический метод	Приложение MathCad
Xa	0.040	0.040	0.040
Xa’	-0.069	-0.069	-0.069
Xa’’	-0.040	-0.040	-0.040
Ya	0.069	0.069	0.069
Ya’	0.040	0.040	0.040
Ya’’	-0.069	-0.069	-0.069
Xb	-0.125	-0.125	-0.125
Xb’	-0.102	-0.102	-0.102
Xb’’	0.025	0.025	0.025
Yb	0.520	0.520	0.520
Yb’	0.028	0.028	0.028
Yb’’	-0.048	-0.048	-0.048
Xd	-0.067	-0.067	-0.067
Xd’	-0.182	-0.182	-0.182
Xd’’	0.044	0.044	0.044
Yd	0.732	0.732	0.732
Yd’	0.050	0.050	0.050
Yd’’	-0.086	-0.086	-0.086
Xe	0.030	0.030	0.030
Xe’	-0.172	-0.172	-0.172
Xe’’	0.027	0.027	0.027
Ye	0.705	0.705	0.705
Ye’	0.087	0.087	0.087
Ye’’	-0.095	-0.095	-0.095
Yf	0.411	0.411	0.411
Yf’	0.244	0.244	0.244
Yf’’	0.064	0.064	0.064
Fi2	290.157	290.157	290.157
Fi2’	0.072	0.072	0.072
Fi2’’	-0.142	-0.142	-0.142
Fi3	74.550	74.550	74.550
Fi3’	0.377	0.377	0.377
Fi3’’	-0.131	-0.131	-0.131
Fi4	132.535	132.535	132.535
Fi4’	0.582	0.582	0.582
Fi4’’	0.218	0.218	0.218

План скоростей при q=109.0131⁰

План ускорений при q=109.0131⁰

II Часть

II.1.1 Введение

Выходное звено 5 совершает поступательное движение, поэтому рабочая нагрузка задается в виде нагрузочной диаграммы.

При построении зависимости P(φ) учитывается два обстоятельства:

а) рабочему ходу соответствует больший угол поворота кривошипа , а холостому ходу – меньший угол поворота

б) знак рабочей нагрузки противоположен знаку скорости выходного звена 5.

График зависимости рабочей нагрузки от угла поворота кривошипа:

	(м) Ход поршня

 

	(м) Диаметр поршня

 

	(Па) Рабочая нагрузка

 

	(Па) холостая нагрузка

 

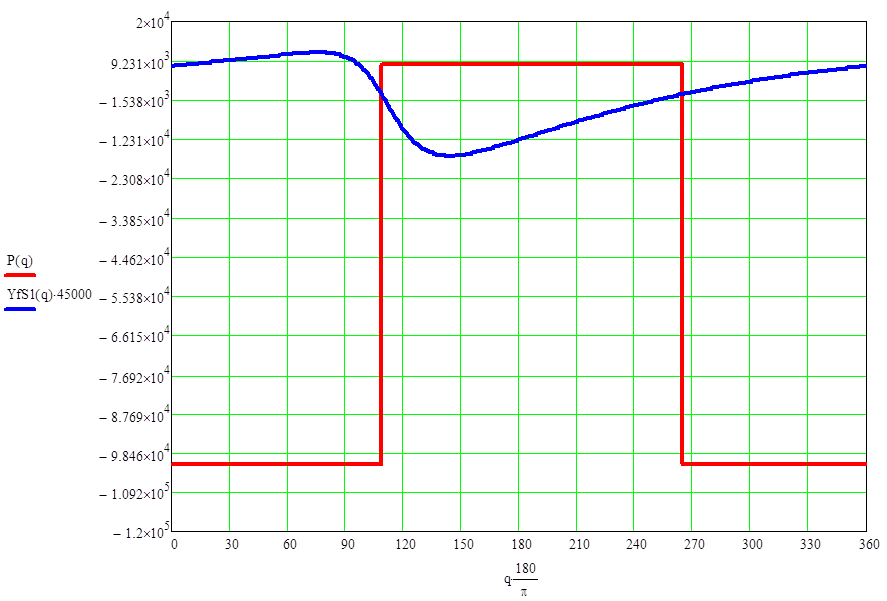
Рисунок II.1.1,12

II.1.2 Кинетостатический расчет механизма

Задачей кинетостатического расчета механизма является определение реакций в кинематических парах и движущего момента Q с учетом сил инерции подвижных звеньев.

Массы звеньев, совершающих вращательные движения определим по зависимости: , где  - длина звена,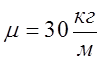 - погонная масса.

Тогда:

Осевые моменты инерции вращающихся звеньев определяем по формулам:

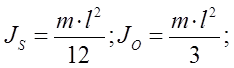
Силы тяжести звеньев определим по формуле:

Координаты центров масс звеньев:

Проекции сил инерции и моменты сил инерции:

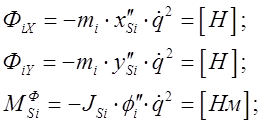
Силы инерции:

Моменты инерции:

Составление и аналитическое решение уравнений кинетостатики

Группа ВВП(звенья 4 и 5):

Рисунок II.1.2 ,13

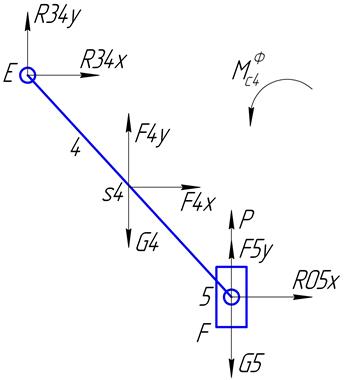
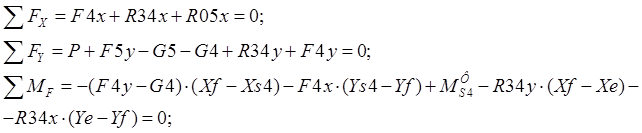
Реакции:

Группа ВВВ(звенья 2 и 3):

Рисунок II.1.2 ,14

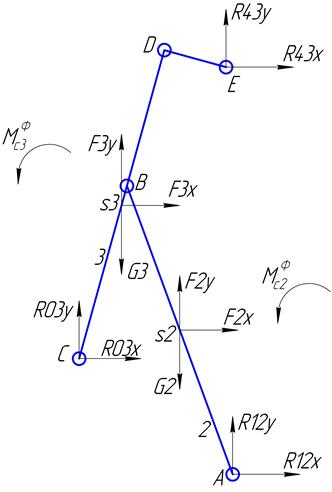
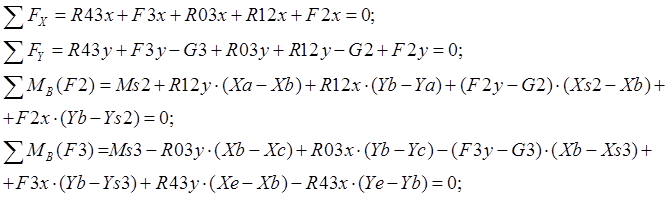
Реакции:

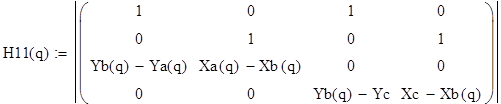
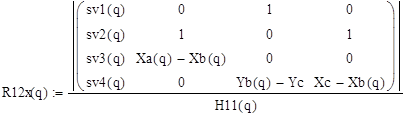
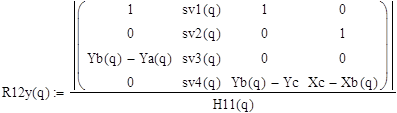
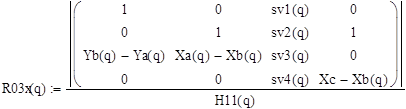
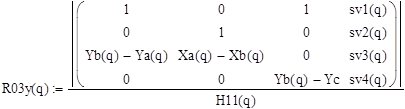
Звено 2:

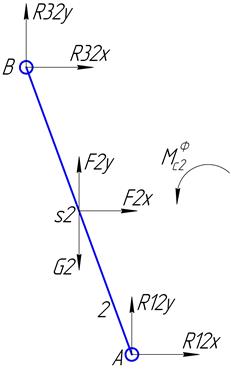
Рисунок II.1.2 ,15

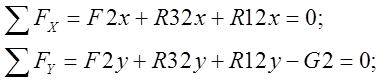
Реакции:

Звено 5:

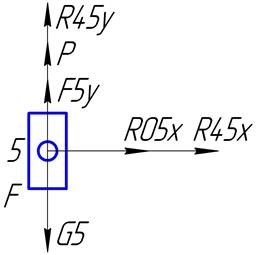
Рисунок II.1.2 ,16

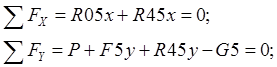
Реакции:

Кривошип:

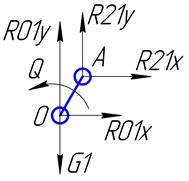
Рисунок II.1.2 ,17

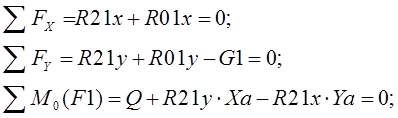
Реакции:

С помощью общего уравнения динамики:

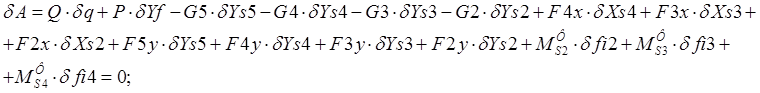
Определим движущий момент (проверка):

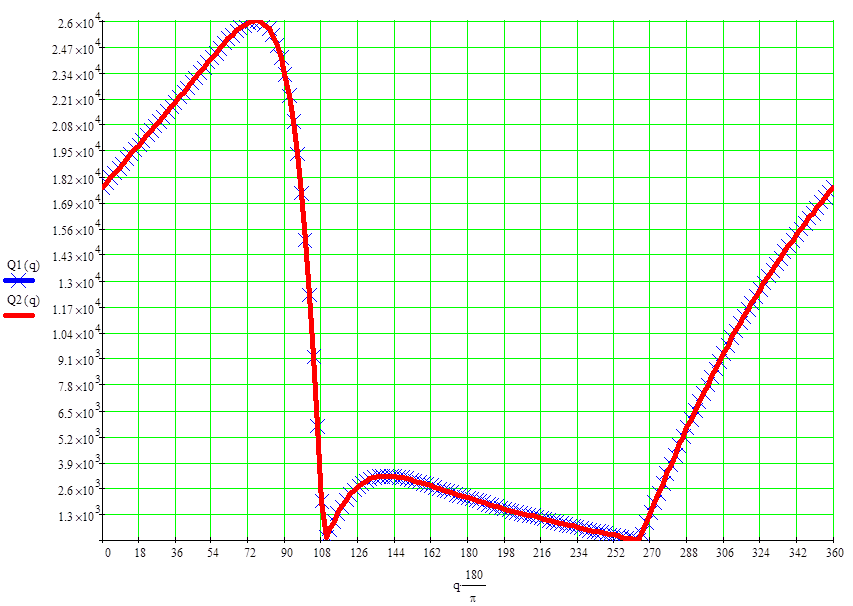
Рисунок II.1.2 ,18