Исследование рычажного механизма: Порядок выполнения курсовой работы по теории механизмов и машин

Министерство образования Российской Федерации

САНКТ-ПЕТЕРБУРГСКИЙ

Порядок выполнения курсовой работы по теории механизмов и машин

ИССЛЕДОВАНИЕ РЫЧАЖНОГО МЕХАНИЗМА

Санкт-Петербург

2002

Часть 1

 Структурный, геометрический и кинематический

анализ механизма

I. Алгоритм структурного анализа механизма

1.  Составить структурную схему механизма, используя условные обозначения кинематических пар и звеньев без учета их геометрических размеров. Пронумеровать и назвать звенья механизма.

2.  Построить граф механизма, в котором звенья соответствуют вершинам, а кинематические пары - ребрам. Номер вершины совместить с номером звена. Число ребер, соединяющих смежные вершины, должно совпасть с    - подвижностью кинематической пары.

3.  Отметить утолщенными линиями корни графа – ребра, соответствующие n входам механизма.

4.  Определить N – число подвижных звеньев механизма, 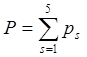- количество кинематических пар механизма (- число кинематических пар s – й подвижности) и 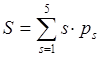- суммарное число подвижностей всех кинематических пар (число ребер графа).

5.  Найти число независимых контуров графа – замкнутых цепей, отличающихся от других цепей хотя бы одной вершиной или ребром.

6.  Определить степень подвижности механизма , где для пространственного механизма В=6; для плоского механизма В=3.

7.  Проверить выполнение условия , являющегося признаком нормального механизма.

8.  При  удалить из механизма лишние входы или звенья, вносящие лишние подвижности и избыточные связи, а из графа – соответствующие им корни или вершины и ребра.

9.  В окрестности 0 – вершины (стойки) выделить подграф, соответствующий структурной группе механизма. Укажем на числовой признак такого подграфа. Из структурной формулы следует

т.е. разность между суммарным числом ребер подграфа и числом                                  

корневых ребер подграфа (входов группы), равная числу некорневых                

(тонких) ребер, кратна шести (для пространственного механизма), трем    

 (для плоского механизма) или равна нулю при (для открытой    

кинематической цепи типа «дерево»). Последовательно из графа выделить

все подграфы, соответствующие структурным группам механизма.

10.  Построить структурный граф механизма, в вершинах которого отметить             

      количество звеньев в найденных группах и число входов, входящих в них.  

Порядок присоединения структурных групп к стойке указать стрелками.   

Если к предшествующей группе присоединяются одновременно несколько 

групп, образуя структурный слой, то их следует отметить на одном уровне.

II. Алгоритм геометрического анализа механизма

1.  Путем размыкания некоторых кинематических пар привести замкнутую кинематическую цепь механизма к открытой кинематической цепи типа "дерево" ( в механизмах второго класса рекомендуется размыкать внешние кинематические пары структурной группы, не связанные со стойкой).

2.  На графе механизма обозначить относительные координаты, определяющие положение каждого звена "дерева" по отношению к предыдущему. При этом наряду с входными координатами дополнительно ввести координаты, называемые групповыми. Число групповых координат должно совпасть с числом разомкнутых связей.

3.  На структурном графе обозначить входные и выходные координаты структурных групп.

4.  Составить уравнения геометрического анализа (групповые уравнения), связывающие входные и выходные (групповые) координаты структурных групп.

5.  Решить групповые уравнения. При этом следует выделить основное решение и отбросить побочные решения, соответствующие иным сборкам звеньев.

6.  Выразить абсолютные угловые координаты звеньев через относительные.

7.  Исследовать функции положения выходных звеньев структурных групп:

 а.) Установить, при всех ли заданных входных координатах механизма определяются эти функции, а значит, - существует механизм и структурные группы.

      Условия существования структурных групп выражаются соответствующими неравенствами, отображающими следующие ограничения: подкоренные выражения должны быть неотрицательными; синусы и косинусы определяемых углов по модулю не должны превышать единицу.

 б.) Получить аналитические выражения первых и вторых производных от функций положения по входной координате (по входным координатам). Выразить якобианы групповых уравнений через групповые координаты.

 в.) Определить условия, при которых первые и вторые производные от функций положения не существуют, т.е. найти особые положения структурных групп. Изобразить структурные группы в особых положениях.

 г.) Изобразить одноподвижный механизм в особых положениях и получить условия их реализации.

 д.) Получить условия существования кривошипа.  

 е.) Найти все экстремумы функций положения.

 ж.) Построить кинематическую схему механизма, т.е. подобрать ее постоянные геометрические параметры (длины звеньев, координаты неподвижных шарниров, углы наклона неподвижных составляющих и т.д.). Эти параметры должны удовлетворять условиям существования групп.

 з.) Определить наибольшее и наименьшее значение функции положения выходного звена, соответствующие крайним положениям механизма. Изобразить механизм в крайних положениях.