10. Решение обыкновенных дифференциальных уравнений первого порядка методом Эйлера
10. 1 Цель работы
Целью данной работы является изучение численного метода Эйлера решения обыкновенных дифференциальных уравнений первого порядка, приобретение навыков использования соответствующих численных методов с применением программных средств автоматизации вычислений.
Также рассмотрены модификации метода Эйлера.
10.2 Задание
Таблица 10.1
|
№ |
ОДУ |
Точное решение |
a |
b |
Δdop |
|
1 |
|
|
0.2 |
1.6 |
0.05 |
|
2 |
|
|
0.2 |
4 |
0.5 |
|
3 |
|
|
0.5 |
3 |
0.9 |
|
4 |
|
|
1 |
4 |
0.01 |
|
5 |
|
|
0 |
2 |
0.02 |
|
6 |
|
|
1 |
3 |
0.02 |
|
7 |
|
|
0 |
2 |
0.015 |
|
8 |
|
|
0.5 |
4 |
0.003 |
|
9 |
|
|
0.5 |
4 |
0.07 |
10.3 Теоретические сведения
Дифференциальные уравнения - это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. Эти уравнения включают соотношения между искомыми функциями и их производными.
Определение : Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (далее чаще используется сокращение ОДУ).
ОДУ 1 – го порядка, разрешенное относительно старшей производной, может быть записано в виде
![]() (1)
(1)
Решить (или проинтегрировать) дифференциальное уравнение - значит определить неизвестную функцию на определенном интервале изменения ее переменных.
Решением (или интегралом) уравнения (1) называется всякая дифференцируемая функция y = j(x) , удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в уравнение (1) оно обращается в тождество. График решения ОДУ называется интегральной кривой этого уравнения.
Общее решение ОДУ может быть записано в виде
y = j(x)+const , (2)
Частным решением ОДУ называется всякое решение, полученное из общего при определенных значениях произвольных постоянных, входящих в общее решение. Произвольные постоянные определяются из заранее заданных условий. Условия могут быть начальными или граничными.
Постановка соответствующей задачи Коши для ОДУ первого порядка
у' (x)=f (y(x),x) (4)
и одно начальное условие при x=x0y(x0)=y0 (5)
Требуется определить функцию y(x) на интервале от x0 до b .
Приближенные методы решение ОДУ можно разделить на две группы:
- аналитические методы, дающие приближенное решение в виде аналитического выражения;
- численные методы, дающие приближенное решение в виде таблицы.
Метод Эйлера относится к численным методам решения ОДУ.
Метод Эйлера.
.
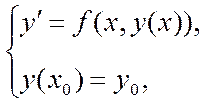 Пусть дано ОДУ первого порядка
Пусть дано ОДУ первого порядка
с начальным условием
Требуется найти решение на отрезке [a , b] .
|
|
Семейство интегральных кривых ( сплошная и пунктирные линии) представляет общее решение дифференциального уравнения. |
Разобьем отрезок [a,b] на n равных частей, получим
последовательность узлов x0, x1, . . . , xn , где xi
= x0 +i×h (i=0,1,…,n), а ![]() - шаг интегрирования. Точное решение
(сплошная линия) в соответствии с начальными условиями проходит через точку А0
с координатами (x0,y0). Заменим точное решение y
=j(x) касательной к интегральной кривой в
точке А0
при
x=x0 (рис.10.1)
- шаг интегрирования. Точное решение
(сплошная линия) в соответствии с начальными условиями проходит через точку А0
с координатами (x0,y0). Заменим точное решение y
=j(x) касательной к интегральной кривой в
точке А0
при
x=x0 (рис.10.1)
При x=x1 получим точку А1 с ординатой y1=y0+h×tga0. Но tga0=y’(x0) и, учитывая (4), получим y1=y0+h×f(x0,y0), где f(x0, y0) - функция, характеризующая наклон касательной в точке А0. Выполнив аналогичную процедуру в точке А1, найдем ординату точки А2 :
y2=y1+h×f(x1, y1).
В общем случае дляi-ой точки можно записать yi+1=yi+h× f(xi ,yi ). Глобальная (суммарная) ошибка в конце отрезка [a, b] будет О(h),
Первый модифицированный метод Эйлера.
Сначала на каждом i -ом шаге, как и в методе Эйлера, используя наклон касательной в точке Ai (х=xi), вычисляют промежуточное значение yi+1/2 , но не на всей длине шага h , а на его половине в средней точке Ac (х=xi+1/2) каждого интервала [xi , xi+1] (Рис.10.2.):
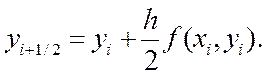
|
|
Затем находят направление
касательной fi+1/2 в середине интервала в точке Ac (х=xi+1/2=xi+h/2) : |
Это направление и принимают за окончательное при
вычислении ординаты точки Ai+1 на всем интервале h от точки Ai: ![]()
Подставив в последнюю формулу два предыдущих
выражения, получим одну результирующую формулу для вычисления ординаты точки Ai+1: 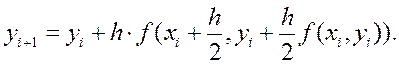
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.