Линейное геометрическое программирование: Лабораторная работа № 14. Вариант № 10

Задание: целевая функция: Z=  

ограничения

условия неотрицательности:

Воспользуемся привчной нумерацией строк и столбцов, начиная с 1

Составяем матрицу коэффициентов, включив в первую и последнюю строки условие неотрцательности

Определяем функцию для построения линий, ограничевающих многогранник допустимых решений, за исключением линий, совпадающих с координатными осями

Определяем функции для составления матрицы аТ коэффицентов линейной системы ограничений и вектор bT ее правых частей для каждой пары пересекающихся линий, включая и координатные оси

Вычисляем координаты точек пересечения ограничивающих линий, используя встроенную функцию lsolve решения СЛАУ для каждой соседней пары пересекающихся линий

Выводим значения координат первых 4 точек пересечения ограничивающих линий

Вводим нулевые значения координатам 6-й точки, соответствующей началу кооринат. Для построения замкнутого контура ограничивающих линий 7-ую точку приравниваем к 1-ой

Составляем вектор коэффициентов целевой функции Z в любой точке

Определяем значение целевой функции Z в любой точке

Определяем функцию вычисления координаты  для посторения целевой функции Z 

Строим график:

-три ограничивающих линий L(1,x)...L(3,x);

-шесть точек пересечения ограничивающих линий ...;

-линии уровня целевой функции LZ(Z(),x), проходящей, например, через ;

-линии уровня целевой функции LZ(Z(),x), проходящей через точку , в которой она будет являться опорной линией, т.к. многогранник допустимых значений будет лежать по одну сторону от нее и значение целевой функции при этом будет максимальным.

Вычисляем значение целевой функции в точке   

В качестве проверки вычисляем значения целевой функции в точках ,  и . Они меньше, чем в точке

Выводим значения координат точки  

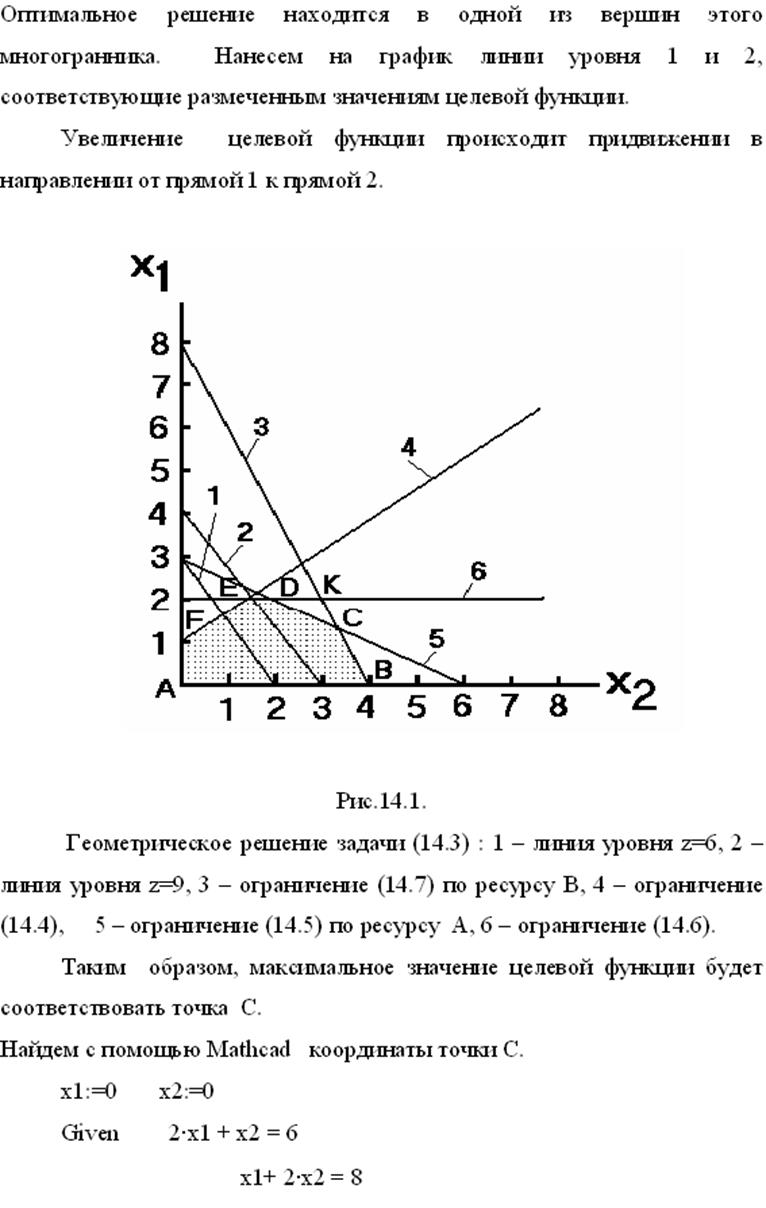
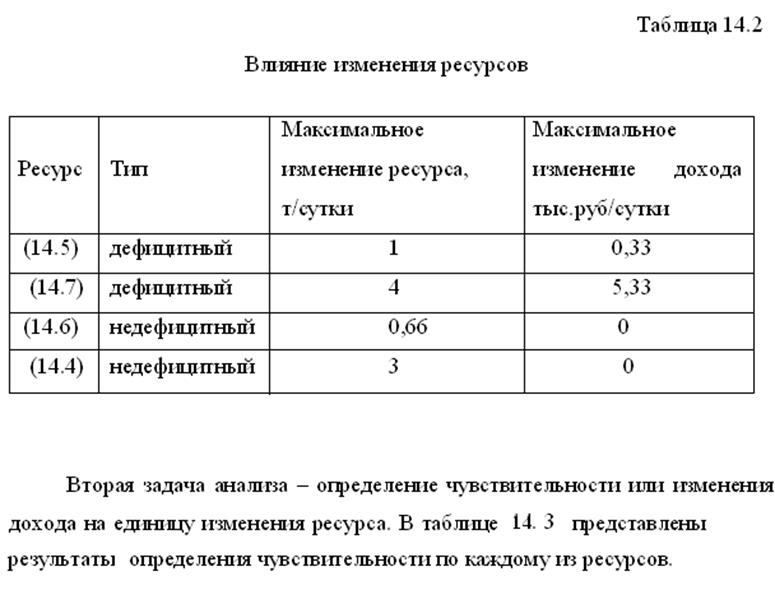
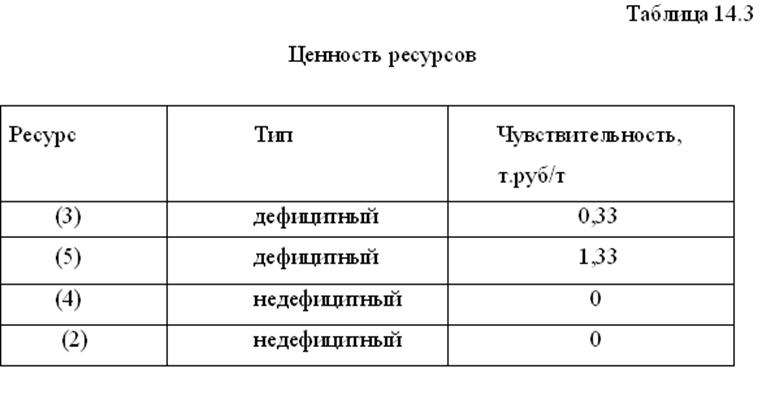
Вывод: максимальное значение целевой функции, равно Z=41, будет при значениях =10 и =-3