Цель работы: 1) изучение методов расчета функции надежности системы с учетом разнообразных связей её элементов; 2) получение навыков декомпозиции произвольных структур анализируемых систем и алгоритмизации задач расчета их надежности; 3) разработка программного обеспечения расчета надежности сложных систем с независимыми элементами, работающими до первого отказа.
ИСХОДНЫЕ ДАННЫЕ К РАБОТЕ
Таблица исходных данных 1. Интенсивность отказа элементов.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
n |
λ |
|
λί, 1/ч |
1/100 |
1/200 |
1/300 |
1/400 |
1/500 |
1/300 |
1/300 |
1/100 |
1/200 |
1/100 |
1/400 |
5,7,10 |
1/400 |
|
1/200 |
1/300 |
1/400 |
1/400 |
1/500 |
1/200 |
1/300 |
1/100 |
1/200 |
1/300 |
1/100 |
6,8,9 |
1/200 |
Рисунок 1 – Схема соединения элементов (вариант №1)
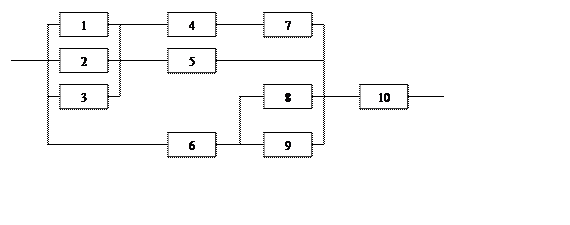 |
1 АНАЛИЗ ПОСЛЕДОВАТЕЛЬНОГО И ПАРАЛЛЕЛЬНОГО СОЕДИНЕНИЯ ЭЛЕМЕНТОВ
При последовательном соединении элементов, приведенном на рисунке 2, отказ одного элемента приводит к отказу всей системы.

Рисунок 2 – Схема последовательного соединения элементов
Функция надежности такой системы вычисляется как:
pс(t) = р1(t)р2(t)…рn(t), (1)
а функция отказа
qc(t) = 1- [(1-q1(t))(1-q2(t))…(1-qn(t))] (2)
В случае показательного закона надежности элементов имеем, что
pi(t) = e –λit , i = (1,n),
где λί = const – интенсивность отказов i – го элемента. Из выражения (1) следует, что:
pс(t) = e –λсt ,
где λс – интенсивность отказов системы, которая вычисляется как
λс(t) = ∑ λί .
Среднее время безотказной работы такой системы будет равно:
Тс = 1/ λс , (3)
Параллельное соединение элементов выбирается в том случае, если отказ системы возникает при отказе всех ее элементов. При этом функция отказов системы определяется как
qc(t) = q1(t) q2(t)…qn(t) (4)
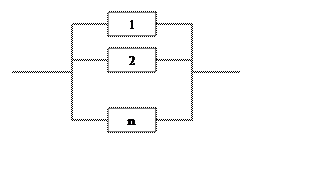 |
Рисунок 3 – Схема параллельного соединения элементов
Функция надежности такой системы будет равна:
рc(t) = 1- [(1-р1(t))(1-р2(t))…(1-рn(t))] (5)
Среднее время безотказной работы системы вычисляется по формуле:
Тс =∫ рс(t) dt. (6)
По условию задания данной лабораторной работы необходимо найти вероятности безотказной работы систем, состоящих из n-блоков, соединенных последовательной и параллельной связью. Результаты расчета Тс, рс(t) этих систем для 3-х значений количества элементов n приведены в таблице 2.
Для последовательного соединения элементов
Таблица 2 – Надежность системы
|
Вер-ть |
Время, t |
||||||||||
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
Р(t), n=5 |
1 |
0.82 |
0.67 |
0.55 |
0.45 |
0.37 |
0.30 |
0.25 |
0.20 |
0.17 |
0.14 |
|
Р(t), n=7 |
1 |
0.74 |
0.55 |
0.41 |
0.30 |
0.22 |
0.17 |
0.12 |
0.09 |
0.07 |
0.05 |
|
Р(t), n=10 |
1 |
0.90 |
0.82 |
0.74 |
0.67 |
0.61 |
0.55 |
0.50 |
0.45 |
0.41 |
0.37 |
Таблица 3 – Вероятность отказов системы
|
Вер-ть |
Время, t |
||||||||||
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
|
Р(t), n=5 |
0 |
0,18 |
0,33 |
0,45 |
0,55 |
0,63 |
0,7 |
0,75 |
0,8 |
0,83 |
0,86 |
|
Р(t), n=7 |
0 |
0,26 |
0,45 |
0,59 |
0,7 |
0,78 |
0,83 |
0,88 |
0,91 |
0,93 |
0,95 |
|
Р(t), n=10 |
0 |
0,1 |
0,18 |
0,26 |
0,33 |
0,39 |
0,45 |
0,5 |
0,55 |
0,59 |
0,63 |
Далее приведены графики функции надежности и функции отказа для 5, 7 и 10 элементов, соединенных последовательно.
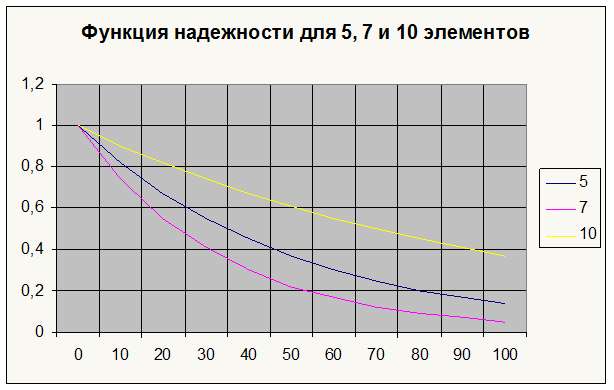 |
|||
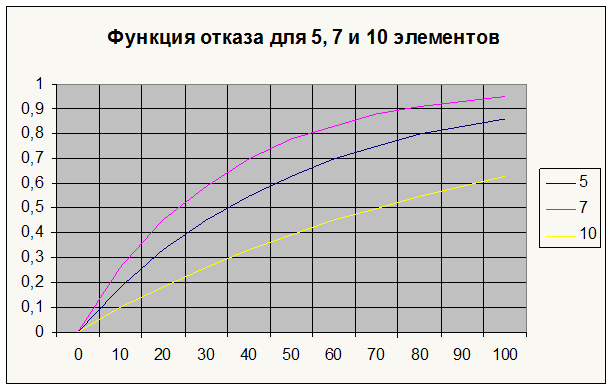 |
|||
Для параллельного соединения элементов
Таблица 4 – Надежность системы
|
Вер-ть |
Время, t |
||||||||||
|
0 |
200 |
400 |
600 |
800 |
1000 |
1200 |
1400 |
1600 |
1800 |
2000 |
|
|
Р(t), n=5 |
1,00 |
0,99 |
0,84 |
0,60 |
0,39 |
0,25 |
0,16 |
0,10 |
0,06 |
0,04 |
0,03 |
|
Р(t), n=7 |
1,00 |
1,00 |
0,96 |
0,80 |
0,59 |
0,40 |
0,26 |
0,17 |
0,11 |
0,07 |
0,05 |
|
Р(t), n=10 |
1,00 |
0,95 |
0,74 |
0,51 |
0,33 |
0,22 |
0,14 |
0,09 |
0,06 |
0,04 |
0,03 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.