Расчет структурной надежности системы (наработка исходной системы составляет 90%)

Цель работы: получение навыков преобразования сложных технических систем и расчета сложных систем с комбинированным соединением элементов, овладение методами повышения надежности систем.

ИСХОДНЫЕ ДАННЫЕ К РАБОТЕ

По структурной схеме надежности системы в соответствии с вариантом задания и по требуемому значению вероятности безотказной работы системы ρ и значениям интенсивности её отказов λ_ί требуется:

1. построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0,1-0,2;

2. определить ρ-процентную наработку системы;

3. обеспечить увеличение ρ-процентной наработки не менее чем в 1,5 раза за счет:

- повышения надежности элементов;

- структурного резервирования элементов системы.

Численные значения параметров

Номер варианта	γ, %	Интенсивность отказов элементов λί · 10-6, 1/ч
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	90	0,1	1,0					0,5	1,0					0,1

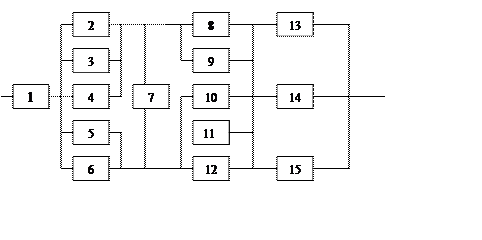
Рисунок 1 – Структурная схема надежности

   

ХОД РАБОТЫ

1. В исходной схеме элементы 2,3 и 4 образуют параллельное соединение. Заменяем их квазиэлементом А, учитывая, что p₂=p₃=p₄, получим

p_A = 1-q₂q₃q₄=1-q₂³=1-(1-p₂)³

2. Элементы 5 и 6 образуют параллельное соединение , заменив которое квазиэлементом В и учитывая, что р₅=р₆=р₂, получим

Р_В= 1-q₅q₆=1-q₂²=1-(1-p₂)²

3.Элементы 8,9 образуют параллельное соединение, заменив которое квазиэлементом С, учитывая, что р₈=р₉=р₂, получим

р_С= 1-q₈q₉=1-q₂²=p_В

4. Элементы 10,11,12 также образуют параллельное соединение, заменив которое квазиэлементом D, учитывая, что р₁₀=р₁₁=р₁₂=р₂, получим

р_D= 1-q₁₃q₁₄q₁₅=1-q₂³=1-(1-p₂)³=p_A

5. Элементы 13,14 и 15 образуют соединение «2 из 3». Так как р₁₃=р₁₄=р₁₅, то для определения ВБР элемента М воспользуемся комбинаторным методом:

Р_m= ∑³_k=2 p_k= ∑³_k=2 C^k₃ p^k₁₃ (1- p₁₃)^3-k= C²₃ p²₁₃ (1- p₁₃)^3-2 + C³₃ p³₁₃ (1- p₁₃)^3-3= = 3!/2!(3-2)! · p²₁₃ (1- p₁₃) + 3!/3!(3-3)! · p³₁₃ (1- p₁₃) - p³₁₃= (3·2·1)/(3·2·1) · p²₁₃ (1- p₁₃)⁰· p³₁₃= 3 p²₁₃ -2p³₁₃   =

Преобразованная схема изображена на рисунке 1.1

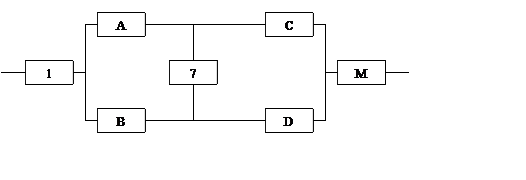
6. Элементы А, В, 7, С, D образуют мостиковую систему, которую можно заменить квазиэлементом N. Для расчета ВБР воспользуемся методом разложения относительно особого элемента, в качестве которого выберем элемент 7. Тогда:

Р_n= p ₇ Р_n ( p ₇=1)+ p ₇ Р_n ( p ₇=0), где

Р_n ( p ₇=1)-ВБР мостиковой схемы при абсолютно надежном элементе 7

Р_n ( p ₇=0)- ВБР мостиковой схемы при отказавшем элементе 7

Преобразование мостиковой схемы при абсолютно надежном и отказавшем элементе 7 изображено на рисунке 1.2.

Рисунок 1.2 Преобразование мостиковой схемы

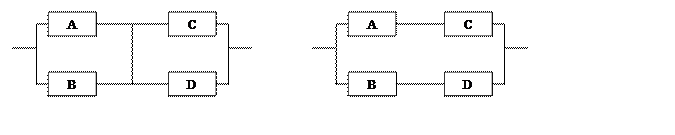
7. Учитывая, что р_В=р_С, р_А=р_D получим:

Р_n= p ₇ [1-(1-p_А)(1-p_В)] · [1-(1-p_С)(1-p_D)] + (1+p₇) [1-(1-p_А p_В)(1-p_С p_D)]

8. После преобразований схема изображена на рисунке 1.3

9. В преобразованной схеме элементы 1, M, N образуют последовательное соединение. Тогда ВБР всей системы

р= р₁ р_N р_M

10. Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то ВБР элементов 1-15 подчиняются экспоненциальному закону:

Р_i = exp(-λ_ί t)

11. Результаты расчетов ВБР элементов 1-15 исходной схемы по формуле Р_i = exp(-λ_ί t) для наработки до 3·10⁶  часов  представлены в виде таблицы 1.

Таблица 1 – Расчет безотказной работы системы

Элемент	λί · 10-6, 1/ч	Наработка t, 106 ч
		0,4	0,5	0,6	0,7	0,8	0,9	1	1,1
1	0,1	0,960789	0,951229	0,941765	0,932394	0,923116	0,913931	0,90483	0,895834
2,6	1	0,67032	0,606531	0,548812	0,496585	0,449329	0,40657	0,367879	0,332871
7	0,5	0,818731	0,778801	0,740818	0,704688	0,67032	0,637628	0,606531	0,57695
8,12	1	0,67032	0,606531	0,548812	0,496585	0,449329	0,40657	0,367879	0,332871
13,15	0,1	0,960789	0,951229	0,941765	0,932394	0,923116	0,913931	0,904484	0,895834
A,D	-	0,9642	0,9391	0,9081	0,8724	0,833	0,791	0,7474	0,7031
B,C	-	0,8913	0,8452	0,7964	0,7466	0,6967	0,6479	0,6004	0,555
N	-	0,99	0,9219	0,9527	0,9193	0,8758	0,823465	0,7642	0,7003
M	-	0,9955	0,9931	0,9902	0,9869	0,9832	0,999362	0,9745	0,9697
P	-	0,9468	0,9219	0,8884	0,8459	0,7948	0,7368	0,6739	0,6083
2′	0,66	0,767974	0,718924	0,673007	0,630022	0,589783	0,552114	0,516851	0,48384
В′, С′	-	0,9729	0,9512	0,944	0,9204	0,9086	0,9024	0,8687	0,8459
N′	-	0,9977	0,9801	0,9871	0,9768	0,9602	0,9539	0,912	0,8729
Р′	-	0,9502	0,9489	0,9401	0,9257	0,9144	0,908	0,8686	0,8438
2′′	-	0,6703	0,6134	0,5488	0,4947	0,4493	0,3894	0,3679	0,3125
С′′, В′′	-	0,9998	0,9901	0,9813	0,9386	0,8724	0,8869	0,8991	0,8831
1′′	-	0,9996	0,9972	0,9966	0,9953	0,9941	0,9929	0,9909	0,9868
N′′	-	0,9999	0,9968	0,9944	0,9602	0,9323	0,9301	0,9271	0,9206
P′′	-	0,9984	0,9897	0,9813	0,9638	0,9411	0,9206	0,8954	0,8879

12. На рисунке 1.4 представлен график зависимости вероятности безотказной работы системы Р от времени наработки t.

Рисунок 1.4

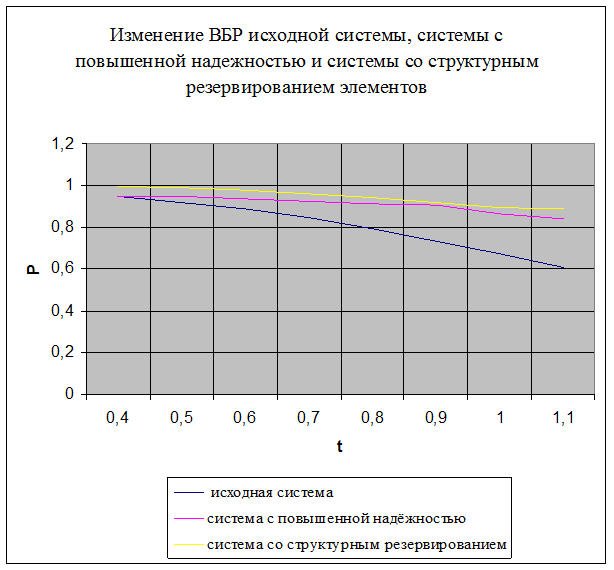
13. По графику находим для γ=90% (Р_γ =0,9) γ- процентную наработку системы Т_γ = 0,6·10⁶  ч.

14. проверочный расчет при  t = 0,6·10⁶  ч показывает, что Р_γ=0,89705≈0,9.

15. По условиям задания повышенная γ- процентная наработка системы Т_γ′ = 1,5 Т_γ =1,5· 0,6·10⁶ = 0,9·10⁶  ч.

16. Расчет показывает, что при t = 0,9·10⁶  ч для элементов преобразованной схемы р₁= 0,913931, р_N = 0,8235,  р_М = 0,9993. Следовательно, из трех последовательно соединенных элементов минимальное значение ВБР имеет элемент N. Следовательно увеличение его надежности даст максимальное увеличение надежности системы в целом.

17. Для того, чтобы при Т_γ′ = 0,9·10⁶ ч система в целом имела ВБР Р_γ=0,9, необходимо, чтобы элемент N имел ВБР:

р_N =р_γ / р₁р_М=0,9/0,913931*0,9993=0,9854.

При данном значении ВБР элемент N надежен, однако, чтобы повысить надежность системы необходимо увеличить надежность двух элементов: 1 и N.

18. Для определения минимально необходимой вероятности безотказной работы элементов необходимо решить уравнение из седьмого пункта относительно р₂ при р_N=0,9854. Поскольку аналитический метод является более сложным, то целесообразнее воспользоваться графическим методом. Для этого по данным таблицы строим график зависимости