Изучение методов расчета функции надежности системы с учетом разнообразных связей её элементов, страница 2

Таблица 5 – Вероятность отказа системы

Вер-ть	Время, t
	0	200	400	600	800	1000	1200	1400	1600	1800	2000
Р(t), n=5	0,00	0,01	0,16	0,40	061	0,75	0,84	0,90	0,94	0,96	0,97
Р(t), n=7	0,00	0,00	0,04	0,20	0,41	0,60	0,74	0,83	0,89	0,93	0,95
Р(t), n=10	0,00	0,05	0,26	0,49	0,67	0,78	0,86	0,91	0,94	0,96	0,97

Далее приведены графики функции надежности и функции отказа  для 5, 7 и 10 элементов, соединенных параллельно.

 

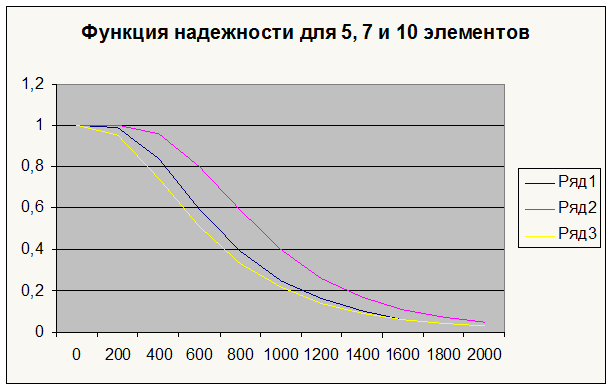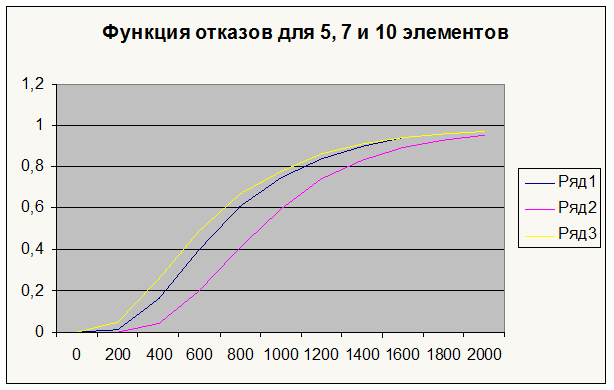В таблице 6 рассчитано среднее время работы до отказа элементов соединённых последовательной и параллельной связью.

Таблица 6 – Среднее время работа до отказа

Тип соединения	Среднее время работы до отказа (Тс), ч
	n=5	n=7	n=10
Последовательное	43.9	33.9	18.3
Параллельное

II ОПРЕДЕЛЕНИЕ НАДЕЖНОСТИ ЗАДАННОГО ВАРИАНТА СХЕМЫ

Индивидуальный вариант схемы представлен на рисунке 1.

1. Блоки 1,2,3 соединены параллельно:

р (А) = 1- [(1-р (1)) (1-р (2))  (1-р (3))]

2. Блоки 4,7 соединены последовательно:

p (В) = р (4) р (7)

3. Блоки 8,9 соединены параллельно:

р (С) = 1- [(1-р (8)) (1-р (9))]

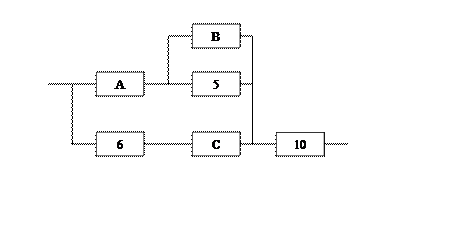
4. Блоки 6 и С соединены последовательно:

p (D) = р (6) р (С) = (1- [(1-р (8)) (1-р (9))] ) * р (6)

5. Блоки В и 5 соединены параллельно:

р (Е) = 1- [(1-р (5)) (1-р (В))] = 1- [(1-р (5)) * ((1- р (4) р (7))]

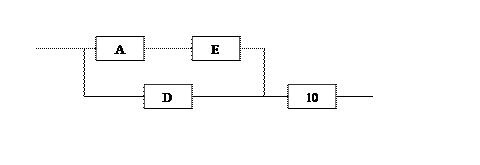
6. Блоки А и Е соединены последовательно:

p (F) = р (A) р (E) = (1- [(1-р (1)) (1-р (2))  (1-р (3))] ) * (1- [(1-р (5)) (1- р (4) р (7))] )

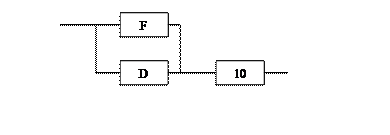
7. Блоки F и D соединены параллельно:

р (G) = 1- [(1-р (F)) (1-р (D))] = (1- [1- (1- [(1-р (1)) (1-р (2))  (1-р (3))] ) * (1- (1- [(1-р (8)) (1-р (9))] ) * р (6)))

8. Блоки G и 10 соединены последовательно:

p (H) = р (G) р (10) = (1- [1- (1- [(1-р (1)) (1-р (2))  (1-р (3))] ) * (1- (1- [(1-р (8)) (1-р (9))] ) * р (6))) * р (10)

Произведем в соответствии с вариантом задания расчет надежности всей системы при трех вариантах (для первого варианта λ_ί= λ, взято из 1ого столбца, для второго варианта  λ_ί = λ, взято из 2 ого столбца, для третьего варианта,  λ_ί = const, в пересечении со строкой «λ»). Результаты расчета приведены в таблицах и на семействе графиков.

Таблица 7 – Надежность системы

Вер-ть	Время, t
	0	100	200	300	400	500	600	700
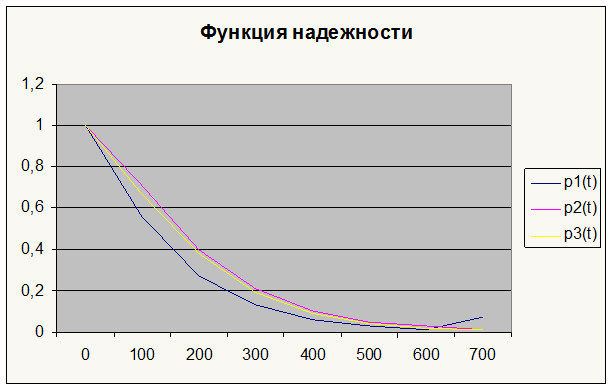
Р(t), 1	1,00	0,56	0,27	0,13	0,06	0,03	0,01	0,07
Р(t), 2	1,00	0,71	0,40	0,21	0,10	0,05	0,03	0,01
Р(t), const	1,00	0,67	0,38	0,19	0,09	0,04	0,02	0,01

Таблица 8 – Вероятность отказа системы

Вер-ть	Время, t
	0	100	200	300	400	500	600	700
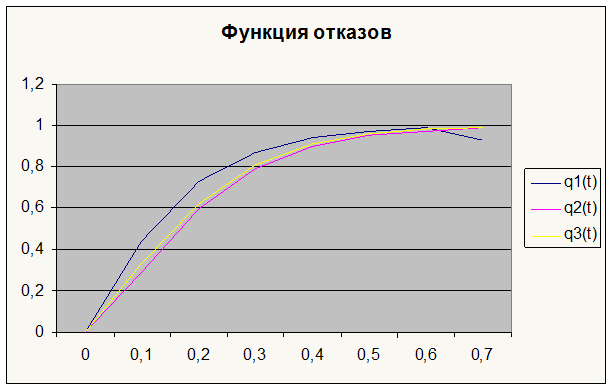
Q(t), 1	0,00	0,44	0,73	0,87	0,94	0,97	0,99	0,93
Q(t), 2	0,00	0,29	0,60	0,79	0,90	0,95	0,97	0,99
Q(t), const	0,00	0,33	0,62	0,81	0,91	0,96	0,98	0,99

Далее приведены графики функции надежности и функции отказа  для трех вариантов.

 

 

В таблице 9 рассчитано среднее время работы до отказа элементов для трех вариантов значений λ.

Таблица 9 – Среднее время работа до отказа

Среднее время работы до отказа (Тс), ч
P(t)1	P(t)2	P(t)3
105.5	127.9	128.5

ВЫВОДЫ ПО РЕЗУЛЬТАТАМ РАБОТЫ

Система, состоящая из блоков, соединенных параллельно значительно надежнее системы состоящей из тех же самых блоков, но соединенных последовательно. С увеличением количества блоков надежность последовательной цепи уменьшается, а параллельной увеличивается.

Как видно по среднему времени наработки до отказа наибольшей надежностью обладает система, построенная из элементов pV2. Также анализ графиков показывает, что надежность системы существенно зависит от положения блоков в этой системе.