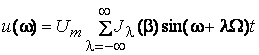Эталоны в области измерения параметров формы и спектра радиосигналов, страница 16

,

где – функция Бесселя первого рода -го порядка.

Амплитуда  – ой спектральной составляющей

.

Бесселева функция является квазипериодической затухающей функцией (см. рис. 6.12), корни которой (пересечение с осью ) табулированы с высокой точностью. Таким образом, регистрируя равенство

,

можно устанавливать , где  – -й “нуль” -ой спектральной со­ставляющей.

Поскольку  и  нам известны,  находится по таблицам, а искомая девиа­ция определяется по формуле  (модулирующая частота  мо­жет быть измерена достаточно точно).

 Практически метод реализуется путем регистрации при помощи спектраль­ного индикатора (например, стандартного анализатора спектра) обращения в нуль той или иной составляющей спектра ЧМ сигнала (рис. 6.11). Обычно для измерения используется составляющая с несущей частотой (), т.е. индициру­ется равенство

,

которое имеет место при  = 2,4048; 5,5201; 8,6537; 11,7915; 14,9309; 18,0711 и т.д.

 

Счетный метод обеспечивает наивысшую точность в области средних и больших индексов модуляции , метод “нулей функции Бесселя” - в области малых ). Метод мгновенной частоты играет роль контрольного [6.4]. Наличие нескольких независимых методов позволяет проводить их взаимное сличение, т.е. контролировать отсутствие неучтенных источников систематической по­грешности.