Эталоны в области измерения параметров формы и спектра радиосигналов, страница 12

Рисунок 6.8 – Закон изменения частоты ЧМ сигнала в функции времени

Если значениям  и соответствуют моменты времени  и  (рис. 6.8), то величины 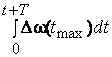 и 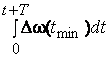 представляют девиации фазы “вверх” и “вниз”. 

В случае гармонической УМ мгновенная частота сигнала

и                    ,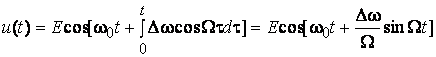

где - девиация частоты;

       – частота модулирующего гармонического колебания;

  –  индекс модуляции, который равен девиации фазы .

Как и при АМ, в случае квазигармонической угловой модуляции с искажен­ным законом модуляции оперируют понятиями парциальных девиаций частоты  (девиаций фазы ), а для оценки нелинейных искажений модулирующей функции используют коэффициент гармоник.[8] Так, для сигнала с искажен­ной УМ

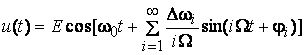
выражения для частоты, девиаций частоты и девиаций фазы имеют вид

;

;

;

;

.

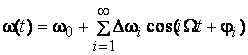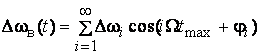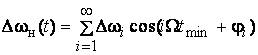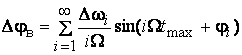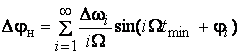Коэффициент гармоник определяется формулой

,

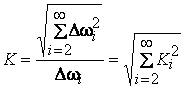где 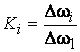 – парциальные коэффициенты -й гармоники.