Разработка оптимальной математической модели процесса получения бутадиен-стирольного каучука методом эмульсионной полимеризации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет химических технологий

Кафедра системотехники

Лабораторная работа № 2

МЕТОДЫ РЕГРЕССИОННОГО И КОРРЕЛЯЦИОННОГО АНАЛИЗОВ

Руководитель:

________________Г.И. Сорокина

(подпись)

_______________________

(оценка, дата)

Разработал:

Студент группы 64-4

Осадчая О.В.

Михальцевич А.Н.

 (подпись)   

__________________________ (дата)

Красноярск, 2007

Методы корреляционного анализа

Условие задачи

Методом множественной корреляции разработать оптимальную математическую модель процесса получения бутадиен-стирольного каучука методом эмульсионной полимеризации. В качестве параметра оптимизации (Y) принять выход каучука в %.

На процесс влияют следующие факторы:

Х₁ – температура процесса^{, 0}С;

Х₂ – давление, атм.;

Х₃ – интенсивность перемешивания массы, об/мин;

Х₄ – количество эмульгатора, % от реакционной массы;

Х₅ – количество инициатора, % от реакционной массы.

Таблица 1 – Исходные данные:

№	Х1	Х2	Х3	Х4	Х5	Y
1	3.0	13.5	32.3	61.7	10.0	29.2
2	2.1	13.2	31.0	63.5	9.2	27.8
3	3.3	12.7	33.2	59.5	11.5	31.0
4	3.5	12.5	32.0	63.0	12.8	31.7
5	3.6	12.5	35.0	58.0	10.1	30.5
6	3.8	12.0	32.6	61.5	10.3	32.5
7	4.0	11.5	34.0	60.0	11.5	31.2
8	4.1	12.6	35.8	64.5	15.0	36.4
9	4.2	11.2	34.2	59.7	12.5	32.3
10	4.5	11.0	36.5	55.2	15.0	36.0
11	4.5	10.6	38.0	53.7	16.2	38.0
12	4.7	10.2	35.7	52.6	14.0	34.6
13	4.8	10.0	39.1	55.6	18.0	40.2
14	5.0	9.5	36.3	55.0	16.0	36.8
15	5.0	9.2	37.2	52.5	18.5	39.8

В работе необходимо:

1) методом парной корреляции определить степень влияния факторов Х_i на технологический процесс и степень закоррелированности факторов между собой. Закоррелированные и не влияющие на процесс факторы из дальнейших расчетов исключить.

2) с применением программы множественного корреляционного анализа разработать три математических моделей процесса получения бутадиен -стирольного каучука:

а) линейную

Y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ ……….+ b_nx_n;

б) показательную

Y = b₀ * b₁^x1 * b₂^x2 * b₃^x3 ………..* b_n^xn;

в) степенную

Y = b0 *x₁^b1 * x₂^b2 * x₃^b3…………* x_n^bn

3) проверить качество описания технологического процесса полученными математическими моделями;

4) рассчитать для каждой математической модели коэффициент множественной корреляции (R);

5) из полученных трех математических моделей выбрать наиболее оптимальную математическую модель технологического процесса.

Описание алгоритма расчета

1. Метод парной корреляции

1. Рассчитываем коэффициент парной корреляции Rx_iy и  Rx_iy_j :

Для количественной оценки тесноты стохастической линейной связи между двумя величинами определим выборочный коэффициент парной корреляции (Rx_iy):

Rx_iy =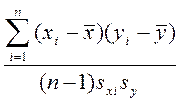,                                                                                                                                                                                  (1.1)

где     ху показывает величины, между которыми определяют тесноту связи;

-значения случайных величин х и у;

 -математические ожидания случайных величин х и у,

которые определим из формул:

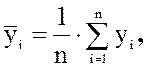                                                                            (1.2)

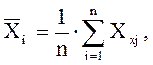                                                                           (1.3)

n- объем выборок х и у;

S_x, S_y -среднеквадратичные отклонения величин х и у, которые

                    определим из формул:

S_y=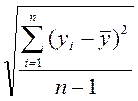,                                                                      (1.4)

S_xi=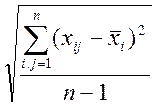,                                                                  (1.5)

Определим , подставляя значения в формулу (1.2):

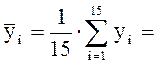 33,87

Определим, подставляя значения в формулу (1.3):

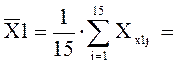 4,007 ; 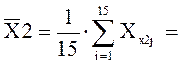   11,48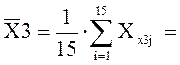0 ;   34,860 ;

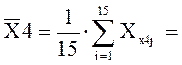58,400 ;  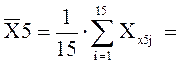   13,373.

Определим S_y, подставляя значения в формулу (1.4):

S_y=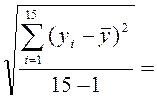  14,770;

Определим S_xi, подставляя значения в формулу (1.5):