1 К точкам ПФЭ 1-го порядка добавляют 2k "звездных" точек, расположенных на координатных осях факторного пространства, на одинаковом расстоянии от центра плана
где α - "звездная" точка, а величина α - "звездное" плечо.
2 Добавляем один или несколько параллельных опытов в центре плана n0.
Полученная матрица неортогональна, так как:
|
|
(2) (3) |
Ортогонализацию столбцов хi2 между собой производим изменением количества опытов в центре плана (n0). Вследствие чего изменяется длина α.
Ортогональность между столбцами x0 и хi2 достигается с помощью преобразований квадратичных столбцов по формуле:
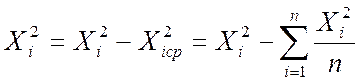 (4)
(4)
По вышеизложенному механизму производится достройка и преобразование матрицы планирования эксперимента.
Для получения математической модели процесса необходимо построить уравнение регрессии второго порядка. В связи с этим проводим регрессионный анализ по первой схеме (при наличии параллельных опытов). Основная задача регрессионного анализа сводится к получению математической модели процесса, проверке адекватности полученной модели и оценке влияния каждого фактора на процесс.
Возможность получения математической модели методом регрессионного анализа определяется следующими условиями:
- точность, с которой задаются независимые переменные хi, не являющиеся случайными, должна быть высокой. К точности измерения параметра оптимизации (у) предъявляют менее жёсткие требования;
- каждая из независимых переменных не должна являться линейной комбинацией остальных независимых переменных;
- интервал между значениями факторов в соседних точках не должен быть меньшим или равным ошибке, с которой задаются этим интервалом.
- значения функции отклика в точках факторного пространства должны определяться независимо друг от друга.
- в исследуемом интервале изменения факторов дисперсии должны быть однородными.
Для получения математической модели процесса необходимо построить уравнение регрессии второго порядка. В связи с этим проводим регрессионный анализ по первой схеме.
Первоначально вычисляем выборочное математическое ожидание:
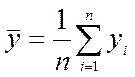 (5)
(5)
где n- количество опытов в матрице;
yi- значение параметра оптимизации;
Определяем выборочную дисперсию:
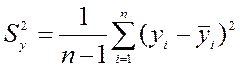 (6)
(6)
|
|
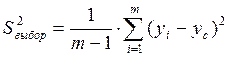 (7)
(7)
![]() , (8)
, (8)
где Sbi2- дисперсия коэффициентов уравнения регрессииi.
n - количество опытов в матрице;
m- количество параллельных опытов;
хi-факторы, влияющие на процесс.
Однородность дисперсии не проверяется.
Вычисляем коэффициенты уравнения регрессии методом наименьших квадратов по формулам:
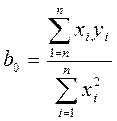 ;
;
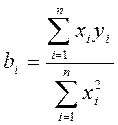 (9)
(9)
где b0- коэффициент уравнения регрессии;
bi- i-тый коэффициент уравнения регрессии;
yi- параметр оптимизации;
хi- факторы, влияющие на технологический процесс.
Проверка значимости коэффициентов уравнения регрессии по критерию Стьюдента:
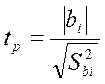 , (10)
, (10)
|
|
Следует отметить, что значимость коэффициентов уравнения регрессии можно оценивать только в исследуемой области факторного пространства. Если фактор оказывается незначимым, то он не оказывает существенного
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.