Выбор метода оптимизации после планов второго порядка

Проверяем значимость коэффициентов уравнения регрессии по критерию Стьюдента:

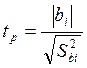,           (6)

где S_bi²- дисперсия коэффициента b_i.

Если t_р > t_табл при α = 0,05, то коэффициент b_i значимо отличается от нуля, то есть фактор, соответствующий этому коэффициенту оказывает существенное влияние на процесс. В противном случае коэффициент b_i незначим, фактор, соответствующий ему, влияния на процесс не оказывает и из уравнения исключается.

Проверяем адекватность уравнения регрессии.

Адекватность – соответствие полученной математической модели реальному процессу.

Проверку проводят по критерию Фишера (F_p)

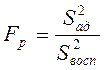,          (7)

где S_ад² – дисперсия адекватности, которая равна:

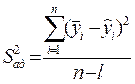,         (8)

где  - расчётный параметр оптимизации;

l- количество значимых коэффициентов b_i.

Полученный F_р сравнивают с F_табл. Если F_р<F_табл – уравнение адекватно. В противном случае уравнение не адекватно и следует перейти к планам более высокого порядка.

В результате расчёта по матрице с преобразованными столбцами х_i² получаем следующее уравнение регрессии:

.

Полученное уравнение нужно преобразовать к такому виду, который реально бы описывал процесс. Коэффициент b₀ пересчитывается по формуле:

.         (9)

В результате проведённого регрессионного анализа и преобразований получаем уравнение регрессии, описывающее данный технологический процесс.

Выбор метода оптимизации после планов второго порядка зависит от вида поверхности отклика.

По виду уравнения регрессии нельзя установить вид поверхности отклика, поэтому вначале проводят исследование поверхности отклика 2-го порядка, то есть нужно получить уравнение регрессии в каноническом виде.

,         (10)

где В - коэффициенты в уравнении регрессии в каноническом виде;

X - канонические переменные, являющиеся линейными функциями факторов х_i;

У_s - расчётное значение выходного параметра в новом начале коорди­нат.

Порядок преобразования уравнения из кодированного в канонический вид (формулы даны для 2-ух факторной модели).

Определяем координаты центра поверхности отклика. То есть необходимо решить систему нормальных уравнений.

(11)

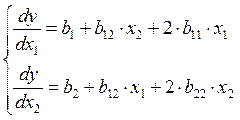
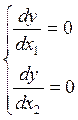
Решая систему, получаем Х_1s, Х_2s (координаты центра поверхности отклика S)

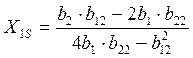,          (12)

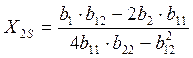.          (13)

Уравнение регрессии в кодированном виде подставляем в него x_1s и х_2s, получаем y_s.

Переносим начало координат в точку S (центр поверхности).

x₁ = x_1s + х'_s                    х₂ = х_2s + х'₂,              у = у_s + у'.                    (14)

Подставим их в уравнение регрессии в кодированном виде и преобразуем:

         (15)

Избавляемся от взаимодействий. Необходимо повернуть оси координат на угол α:

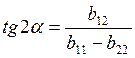.          (16)

Перевод старых координат в новые проводится по формулам:

х₁ =(x₁ + х_1s)соsα-(x₂ +х_2s)sinα;

х₂ =(x₁ +х_1s)sinα + (x₂ +х_2s)соsα.         (17)

Подставив в уравнение (15) значения x₁ и х₂ получим уравнение в каноническом виде.

Вычисление канонических коэффициентов (В).

Для вычисления составляем определитель:

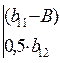
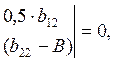                   (18)

         (19)

Решаем квадратное уравнение и получаем переменные В₁₁  и В₂₂. По знакам этих коэффициентов можно определить вид поверхности. В рассматриваемом случае коэффициенты имеют разные знаки, поэтому поверхность отклика имеет вид гиперболического параболоида.

Трудности геометрической интерпретации уравнения регрессии 2 порядка возрастают с увеличением количества факторов и при к>3 дать наглядное геометрическое представление поверхности невозможно.

В этом случае канонические преобразования дают хорошие результаты, если последовательно рассматривать изменения 2-х факторов, застабилизировав остальные на каком – либо уровне. Как правило, это центральный уровень. Не значимые факторы стабилизируют на нижнем уровне.

Выбирают 2 фактора, которые наиболее сильно влияют на процесс, и по ним ведут исследование и оптимизацию технологического процесса, оставшиеся факторы стабилизируют на центральном уровне - их значение в кодированном виде равно 0.