Выбор метода оптимизации после планов второго порядка, страница 2

Оптимизация технологического процесса.

Выбор метода оптимизации процесса после планов 2 порядка зависит от вида поверхности отклика. В данном случае поверхность имеет форму гиперболического параболоида, поэтому необходимо применять для оптимизации технологического процесса метод «Ридж-анализ» и метод движения вдоль канонических осей.

Метод «Ридж-анализ». Этот метод базируется на методе неопределённых множителей Лагранжа. Для выбора оптимальных режимов составляют следующую систему уравнений.

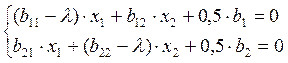,          (20)

где λ – неопределённый множитель Лагранжа. Количество уравнений равно количеству факторов.

Неопределённый множитель задаётся исследователем, но для облегчения вычислений даются интервалы изменения.

Формулы для вычисления x₁ и x₂ имеют следующий вид:

(21)

,

.

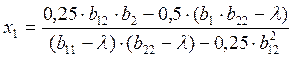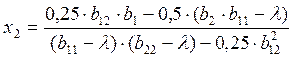В уравнение регрессии в кодированном виде, подставляем значения x₁ и x₂, а другие равны 0 и вычисляем значение у. Смотрим желаемый или не желаемый результат мы получили. Если результат не желаем, то изменяем значение λ.

Значение λ, зависит от типа задачи: в случае задачи на у_mах значение λ, должно быть больше наибольшего коэффициента канонического уравнения регрессии (λ>В_mах). Но  В_mах<λ’.

В_mах<λ’,          (22)

где λ'- параметр Хорля, который вычисляется по формуле

λ'=2(В_mах-b_kk),            (23)

где b_kk – значение коэффициента в кодированном виде. Расчёт по этому методу ведётся в кодированном виде.

Метод движения вдоль канонических осей. Исходными данными в этом методе является уравнение регрессии в каноническом виде. В соответствии с поставленной задачей в канонической системе координат выбираем ось, вдоль которой параметр оптимизации меняется в желаемом направлении и с максимальной скоростью. Для получения у_mах движение происходит вдоль положительной оси. Затем задаваясь различными значениями параметров оптимизации (у), вычисляем соответствующие им режимы и при необходимости проверяем их экспериментально. В связи с симметрией поверхности каждому значению параметра оптимизации соответствуют 2 режима. Поиск оптимального режима без исследования поверхности отклика обычно даёт возможность выделить только один оптимальный режим. Причём исследователь даже не подозревает о существовании 2-го режима, который может оказаться более эффективным для технологии.

Для получения у_мах должно выполняться условие , и выбираем положительную ось движения, а другой фактор стабилизируем на центральном уровне. Из уравнения регрессии в каноническом виде выражаем х:

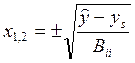.           (24)

Подставляем в формулу желаемый результат и получаем значения факторов х₁₂ в каноническом виде, которые затем переводим в кодированный и натуральный вид вид по формулам.

В результате этого метода получаем характеристики двух оптимальных режимов.

1.3 Входная и выходная информация

Входная информация

Y_i- параметры оптимизации;

1 - количество коэффициентов в уравнении регрессии;

n - общее количество опытов;

t_табл - табличное значение критерия Стьюдента;

к - число факторов;

F_табл - табличное значение критерия Фишера;

Х_Ц - значение центрального уровня факторов;

X_i² - среднее арифметическое;

Х_i - факторы, влияющие на технологический процесс;

λ_i - значения интервалов варьирования.

Выходная информация

Y_ri - расчётные параметры оптимизации;

S_bi - дисперсия коэффициентов уравнения регрессии;

t_расч- расчётное значение критерия Стьюдента;

b_i - коэффициенты уравнения регрессии;

S_aд² - дисперсия адекватности;

S_восп² - дисперсия воспроизводимости;

F_расч - расчётное значение критерия Фишера;

Х_is, Y_s - координаты центра поверхности отклика;

ВB_ii - коэффициенты канонического уравнения;

tg2α - угол поворота осей координат;

L - параметр Хорля;

ВВ_max - максимальное значение коэффициента канонического уравнения;

X_i - значения факторов оптимальных режимов;

Y_i - значения параметров оптимальных режимов.