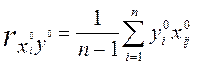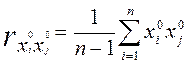Разработка оптимальной математической модели процесса получения бутадиен-стирольного каучука методом эмульсионной полимеризации, страница 3

,               ,                   (2.7)

Вычисленные по этой формуле  коэффициенты корреляции равны коэффициентам корреляции между переменными в натуральном виде.

3. Проверяют существенность влияния факторов на процесс и их закоррелированность методом парной корреляции

2.1. Метод наименьших квадратов

Система нормальных уравнений имеет вид :

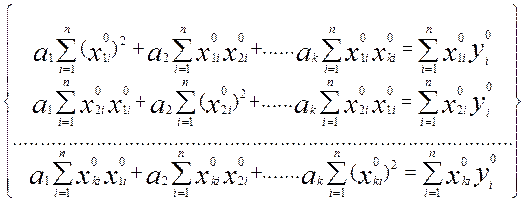
Решая полученную систему, получаем коэффициенты уравнения регрессии в нормированном виде a_i. Перевод уравнения в натуральный вид производим по формулам:

,      ,    

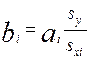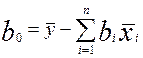Математическая модель будет выражаться следующим уравнением:

y=b₀+b₃x₃+b₅x₅,         

Для показательной модели:

       y=b₀*b₃^x3*b₅^x5,  

Для степенной модели:

          y=b₀*x₃^b3*x₅^b5,                    

Уравнение регрессии получаем в нормированном виде , т.к. исходные данные переведены в нормированный вид. Это делается для упрощения расчетов.

Уравнение регрессии в нормированном виде не имеет  свободного члена b₀ и принимает вид:

Для линейной модели:

 у⁰=а₃х₃⁰+а₅х₅⁰

 Для показательной модели:

 у⁰= а₃^х30*а₅^х50

 Для степенной модели:

        у⁰= х₃^0a3+х₅^0a5  

Коэффициенты уравнения регрессии а_i находят методом наименьших квадратов .

3. Регрессионный анализ

Регрессионный анализ применяем т.к. отсутствует информация о дисперсии воспроизводимости, то есть отсутствуют параллельные опыты, и проводим в следующем порядке (по второй схеме регрессионного анализа):

1. Рассчитывают математическое ожидание столбца y_i:

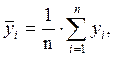                                                                                    (3.1)

2. Рассчитывают дисперсию столбца y_i:

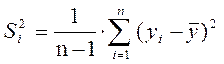,                                                                 (3.2)

3.1. Качество описания математической модели

Проверку адекватности уравнения регрессии произвести невозможно, так как отсутствует дисперсия воспроизводимости. В этом случае можно оценить качество аппроксимации принятым уравнением, сравнив остаточную дисперсию (S ² _ост) и выборочную дисперсию (S ² _y).

          Вычисляют дисперсионное отношение (С):

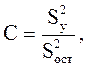                                                                                                                             (3.3)

где     S²_ост – остаточная дисперсия (S²_ост=S²_воспр+S²_ад).

          S²_воспр отсутствует, поэтому S²_ост = S²_ад и вычисляется по формуле:

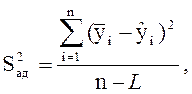                                                                     (3.4)

где     y– расчётный параметр оптимизации;

          L– количество значимых коэффициентов b_i.

Полученные значения С для трёх моделей таковы:

Для линейной модели: С^лин=25.764; Дисперсное отношение (С) сравним с критерием Фишера, взятого из таблицы, F_табл.  находим по степени свободы числителя f_ч=(n-1)=14 и степени свободы знаменателя f_з=(n-L)=14. C^лин>F_табл. , следовательно качество описания процесса полученным уравнением хорошее.

Для показательной модели : C^пок=24.084; C^пок>F_табл, следовательно, качество описания процесса полученным хорошее.

Для степенной модели: С^степ=24.487; С^степ>F_табл, следовательно, качество описания процесса полученным уравнением хорошее.

4. Вычисляем коэффициенты множественной корреляции (Rxy, Rxх).

Подставляя значения в формулу (2.6) определим коэффициенты а_i :

Для линейной модели :

а₁^лин=  0,275  ; a₂ ^лин=  0,730    ;

Для показательной модели:

а₁^пок=  0,624   ; a₂^пок=  0,800   ;

Для степенной модели:

а₁^степ=  0,305   ; a ₂^степ= 0,276    ;

                                                  (4.1)

Коэффициент множественной корреляции показывает силу линейной стохастической связи между параметром у и множеством факторов х_i.

Наши расчётные коэффициенты:

Дл линейной модели:

R^лин=  0,981    ;

Для показательной модели:

R^пок=  1,161    ;