Разработка оптимальной математической модели процесса получения бутадиен-стирольного каучука методом эмульсионной полимеризации, страница 2

S_x1=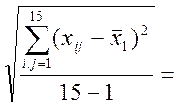0,659,  S_x2= 1,869 ;   S_x3= 5,597;   S_x4= 16,472; S_x5= 8,952 .

Определим Rx_iy, подставим значения в формулу(1.1):

Rx₁y =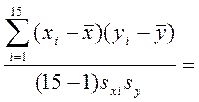0,880; Rx₂y= -0,827; Rx₃y=0,917; Rx₄y=-0,670;  Rx₅y= 0,972 .

Определим Rx_iхj, подставляя значения в формулу(1.1):

Rx₁х₁ =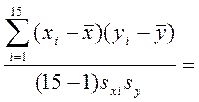1,0 ; Rx₁х₂ = -0,909; Rx₁х₃ =0,855; Rx₁х₄=-0,763; Rx₁х₅ = 0,851;

Rx₂х₁= -0,909; Rx₂х₂= 1,0 ; Rx₂х₃= -0,787; Rx₂х₄= 0,877; Rx₂х₅= -0,831 ;

Rx₃х₁= 0,855; Rx₃х₂=-0,787;   Rx₃х₃= 1,0; Rx₃х₄=-0,760 ;  Rx₃х₅= 0,880 ;

Rx₄х₁= -0,763; Rx₄х₂= 0,857; Rx₄х₃=-0,760; Rx₄х₄= 1,0; Rx₄х₅= -0,669 ;

Rx₅х₁=0,851; Rx₅х₂= -0,831;   Rx₅х₃=  0,880; Rx₅х₄=-0,669;  Rx₅х₅=1,0;

2. Определяем влияние факторов на процесс.

Zx_iy =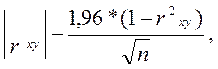                                              (1.6)

Подставляя значения в формулу (1.5) получим:

Zx₁y =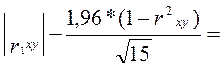 0.765;    Zx₂y =0.666 ;

Zx₃y = 0.835;   Zx₄y = 0.390;    Zx₅y =0.943;

В нашем случае Z_1-5>0, следовательно, в этом случае связь между факторами Х_1-5 и параметрами Y_1-5 существует, то есть факторы Х_1-5 влияют на параметры Y_1-5 а, следовательно, и на технологический процесс.

3. Определение степени закоррелированности факторов между собой.

Аналогично рассчитаем величины Zx_iхj для Rx_iхj, и по ходу расчета будем вести анализ:

Zx₂х₅ =0,831, Zx₂х₅ >0. следовательно, факторы х₂ и х₅ закоррелированы между собой. Присутствие закоррелированных факторов в математической модели недопустимо. Исключаем тот фактор, для которого Rxy по абсолютной величине имеет меньшее значение. |Rх₂y| < |Rx₅y|, поэтому исключаем фактор х₂. Zx₁х₁ =1,0  , Zx₁х₁> 0,   |Rx₁y| < |Rx₅y|, поэтому исключаем фактор х₁. . Zx_iхj =  , Zx_iхj   > 0,   |Rx y| < |Rx y|, поэтому исключаем фактор х₄.

Х₃ и Х₅ – искомые факторы – лишь они будут объектом дальнейшего расчёта.

2. Множественный корреляционный анализ

Исходными данными являются результаты “пассивного” эксперимента, которые представлены в виде матрицы.

Таблица 2.1 – Матрица результатов экспериментов

№	Х3	Х5	Y
1	32.3	10.0	29.2
2	31.0	9.2	27.8
3	33.2	11.5	31.0
4	32.0	12.8	31.7
5	35.0	10.1	30.5
6	32.6	10.3	32.5
7	34.0	11.5	31.2
8	35.8	15.0	36.4
9	34.2	12.5	32.3
10	36.5	15.0	36.0
11	38.0	16.2	38.0
12	35.7	14.0	34.6
13	39.1	18.0	40.2
14	36.3	16.0	36.8
15	37.2	18.5	39.8

Расчеты проводят в следующей последовательности:

1. Перевод исходных данных от натурального вида к нормированному по формулам:

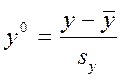,                                                                                (2.4)

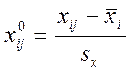,                                                                               (2.5)

где       х_ij⁰, у⁰-нормированные  значения соответствующих факторов и                 параметров оптимизации;

            -математические ожидания соответствующих величин;

           S_у,S_xi- среднеквадратичные отклонения переменных.

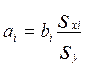                                                                                        (2.6)

2.  Вычисление коэффициентов парной корреляции.

Для нормированных величин имеем:

,              ,       ,     

Поэтому выборочный коэффициент парной корреляции при этом вычисляют по формуле: