Функциональное диагностирование дискретных систем, страница 9

          По базовой функции строятся быстродействующие w/p–СПТ на основе ее разложения на две функции  и , каждая из которых также представляет собой объединение конъюнкций ранга w. Обозначим через ,  и  множества всех слов или соответствующих им конъюнкций кодов соответственно pCw, pC(w+1), pC(w–1). Будем считать, что конъюнкция  ранга w покрывает конъюнкцию  ранга w + 1, если  составляет часть .

          Тестер w/p–СПТ отвечает свойствам контроля входного вектора и самопроверки, если выполняются следующие условия:

          каждая конъюнкция ранга w из множества  должна входить в одну из функций  или , причем только в одну из них;

          каждая конъюнкция ранга w + 1, входящая в множество , должна покрываться хотя бы одной конъюнкцией, включенной в функцию , и хотя бы одной конъюнкцией, включенной в функцию ;

          каждая конъюнкция ранга w – 1, входящая в множество , должна покрывать хотя бы одну конъюнкцию, включенную в функцию , и хотя бы одну конъюнкцию, включенную в функцию .

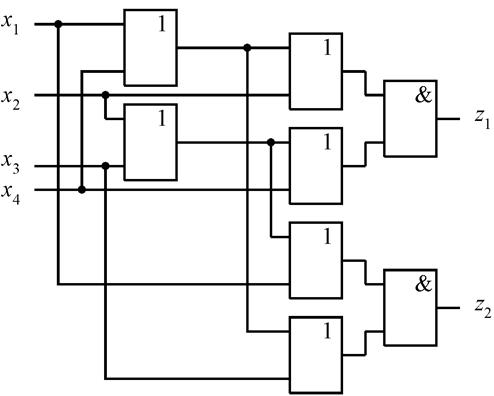
На рис. 6.21 приведена схема 2/4–СПТ, реализованная по функциям

,

.

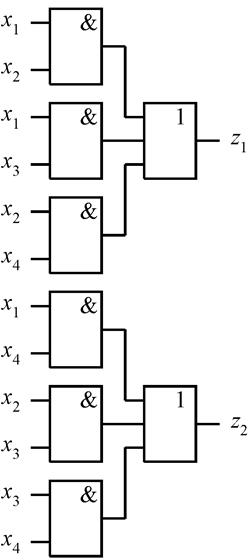
Рис.6.21. Схема двухуровневого 2/4-СПТ

Двухуровневые тестеры, обладая максимальным быстродействием (r = 2), имеют большую сложность (L = (w +1) ) и требуют для своей проверки все слова кода (t = ). Кроме того, двухуровневые тестеры могут быть построены не для всех равновесных кодов.

Универсальным для построения тестеров является принцип преобразования кодов. Он позволяет строить многоуровневые схемы тестеров, что уменьшает их сложность. В этом случае заданный код pCw  преобразуется  в  код  2C1  в  несколько  этапов  по  схеме pCw ®  ®  ® … ® ® 2C1 (рис. 6.22).

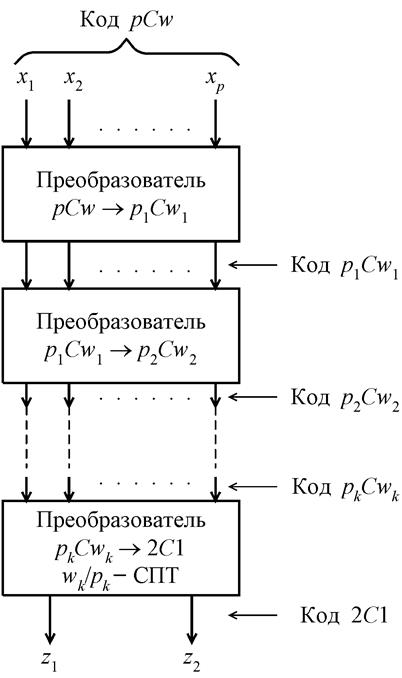
Рис.6.22. Структурная схема тестера

Преобразователи, входящие в СПТ, должны удовлетворять следующим требованиям. Каждый преобразователь должен обладать свойствами контроля входного вектора и самопроверки. Данные свойства аналогичны соответствующим свойствам СПТ. А именно, на выходе преобразователя  формируется слово кода , еcли на его вход поступает вектор кода ; в противном случае формируется вектор, не принадлежащий коду . Для любой одиночной неисправности преобразователя существует слово кода , при котором на выходе устанавливается вектор, не принадлежащий коду . Кроме того, необходимо, чтобы на выходе каждого преобразователя в процессе нормального функционирования формировалось такое множество кодовых векторов, которое составляет проверяющий тест последующего преобразователя. На рис. 6.23 приведена схема 3/4–СПТ, основанная на трехкаскадном преобразовании кода по схеме 4С3 ® 4С1 ® 4С2 ® 2С1.

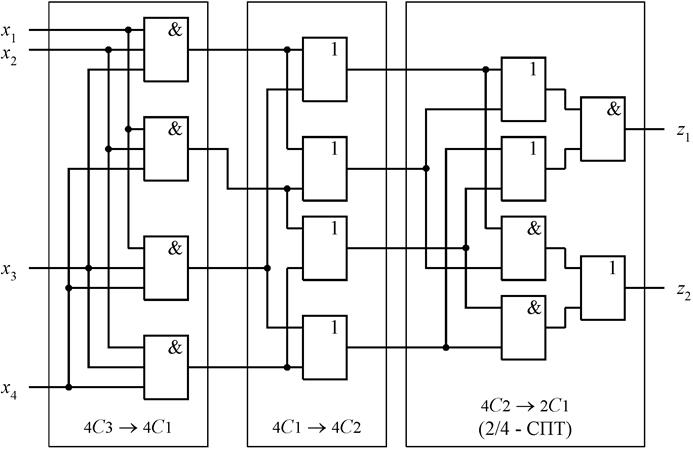
Рис.6.23. Схема 3/4-СПТ

Особый класс составляют 2wCw-коды. Тестеры для таких кодов описываются двумя пороговыми функциями вида , которые принимают значение 1 на наборах входных переменных, имеющая вес w и более. Многоуровневая пороговая цепь строится следующим образом. Множество входных переменных функции В разбивается на два непустых подмножества  и , содержащих соответственно  и  переменных (). Функция, описывающая пороговую цепь,

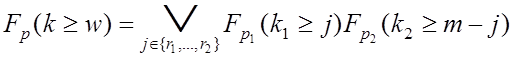,           (6.4)

где , .

          Например, для случая, когда p = 4 и w = 2, образуем подмножества  и . Тогда  =  = 2,  = 0,  = 2. В соответствии с формулой (6.4) пороговая цепь описывается функцией

.

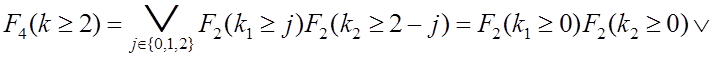
          Функции  и , описывающие структуру  СПТ:

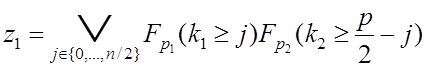;                  (6.5)

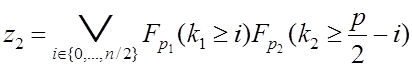,                   (6.6)

где переменная jпринимает значения, соответствующие нечетным числам, а переменная i – четным числам.

          Определим функции  и  для 3/6-СПТ. Множество входных переменных  делим на подмножества  и . Используя формулы (6.5) и (6.6), получим

;

.

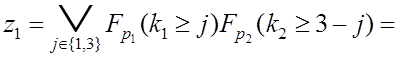
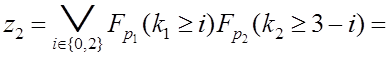
          Схема 2/4-СПТ, приведенная на рис. 6.8, также построена по формулам (6.5) и (6.6).

          С точки зрения построения СПТ особый класс составляют также pC1-коды. Тестеры для них не могут быть построены с использованием формул (6.3)–(6.6). Они реализуются на основе преобразования кодов. Так в схеме рис. 6.23 два правых блока представляют собой 1/4-СПТ, построенный по схеме 1/4 ® 2/4 ® 1/2. Но наибольшее применение на практике нашел каскадный принцип построения 1/р-СПТ. Для любого значения р тестер может быть собран соединением между собой тестеров 1/4-СПТ (рис. 6.24) и 1/5-СПТ (рис. 6.25).