Функциональное диагностирование дискретных систем, страница 10

Рис.6.24. Схема 1/4-СПТ

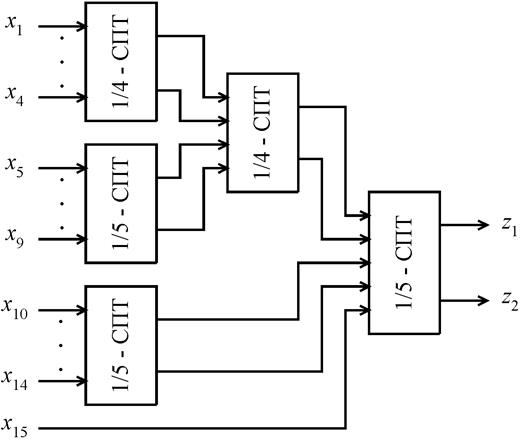
Рис.6.25. Схема 1/5-СПТ

 В схему 1/15-СПТ (рис. 6.26) входят два тестера 1/4-СПТ и три тестера 1/5-СПТ.

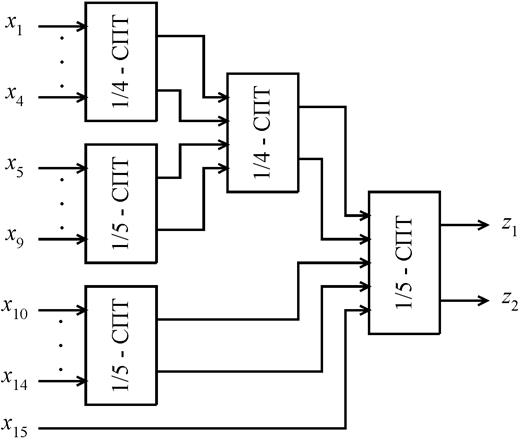
Рис.6.26. Схема 1/15-СПТ

Если на вход тестера поступает слово кода 15С1, в котором  = 1, то на выходе 1/4-СПТ первого уровня схемы устанавливаются сигналы 01 или 10, а на выходах тестеров 1/5-СПТ первого уровня – сигналы 00. В результате сигналы 10 и 01 устанавливаются на выходах 1/4-СПТ второго уровня схемы и на выходах 1/5-СПТ  и . Если на входы схемы поступает некодовое слово, все разряды которого имеют значение 0, то на выходах всех СПТ и на выходах ,  устанавливаются значения 00. Если на вход схемы поступает некодовый вектор с весом  1, то на выходах ,  устанавливаются значения 11. Например, при подаче вектора, в котором  =  =1, на выходах 1/5-СПТ первого уровня устанавливаются значения 10 или 01. В результате такие же значения устанавливаются на выходе 1/4-СПТ второго уровня и на вход выходного 1/5-СПТ поступают два сигнала логической 1, что вызывает установление значений  =  = 1.

          Так как любой кодовый вектор равновесного кода содержит одно и то же число единиц, то детектор кода может быть также построен на основе прямого счета единиц, как это показано на рис. 6.27.

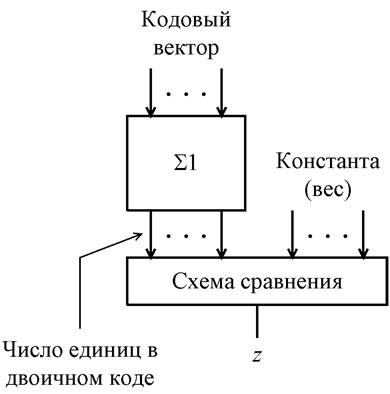
Рис.6.27. Детектор равновесного кода

 В данном случае кодовый вектор подается на вход счетчика единиц , на выходе которого формируется вектор, соответствующий числу единиц в двоичном коде. Он сравнивается с заданным весом, который подается на схему сравнения в виде вектора-константы. Однако, такая структура не может быть реализована в виде самопроверяемой схемы, так как подача на входы схемы констант исключает возможность проверки связанных с этими входами элементов.

          При построении самопроверяемых схем тестеров используются свойства pCw-кодов. Наиболее просто СПТ реализуются для 2wCw-кодов. Рассмотрим, например, код 14С7. Разобьем множество входных переменных на две равные группы:  и . В схеме, показанной на рис. 6.28, отдельными счетчиками  осуществляется подсчет числа единиц в каждой группе.

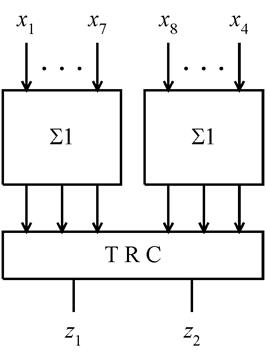
Рис.6.28. Структура 7/14-СПТ

 В табл. 6.8 приведены четыре возможных случая сочетаний чисел единиц в группах  и . Так, если группа  не содержит переменных x = 1, то группа  будет содержать 7 таких переменных и т.д. Из таблицы видно, что во всех случаях на выходах счетчиков  формируются противоположные двоичные векторы. В структуре СПТ этот факт фиксируется при помощи схемы TRC. Если входной вектор имеет вес, не равный заданному, то векторы на выходах счетчиков  не обладают указанным свойством. Например, если группы  и  содержат  2 и 6 единичных переменных соответственно, то формируются векторы 010 и 110.

          Если вес кода , то при подсчете числа единиц в группах  и   можно получить противоположные векторы путем суммирования полученного при подсчете числа с некоторой константой. Для 11С5-кода  получим  множества    и  .   В  табл. 6.9   приведены   три  возможных  случая

                                                                                       Т а б л и ц а   6.8

сочетаний чисел единиц в группах  и , а также результаты сложения их с двоичной единицей (в столбцах  + 1). Сумматоры для сложения двоичных чисел с константами реализуются схемами без избыточных элементов,  что позволяет строить самопроверяемые тестеры.

Т а б л и ц а   6.9

6.5. Контроль по коду с суммированием