Функциональное диагностирование дискретных систем, страница 13

тарных счетчиков единиц блока А.  На  рис. 6.35 приведена диаграм-

ма, на которой проиллюстрирован принцип построения генератора на примере генератора на 11 входов.

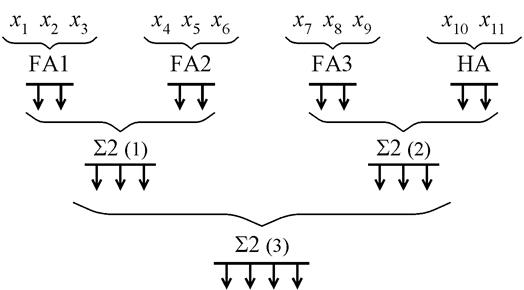
Рис.6.35. Структура генератора на 11 входов

Тройки входов (,,), (,,) и (,,) объединяются сумматорами FA1, FA2 и FA3, а входы (,) – полусумматором НА. Двоичные векторы, формируемые на выходах FA1 и FA2, складываются при помощи сумматора двоичных чисел . Аналогично на выходе  образуется результат сложения векторов с выходов FA3 и НА. На выходах  и  формируются трехразрядные двоичные числа, которые складываются сумматором . На выходе  образуется четырехразрядный двоичный вектор, которым отражается число единиц, присутствующих на 11 входах генератора.

          Сложение двух двоичных чисел осуществляется также при помощи FA и НА. Для сложения двух разрядов устанавливается полусумматор, а трех разрядов – полный сумматор. Необходимость сложения трех разрядов возникает при наличии сигнала переноса от сложения предыдущего разряда. В табл. 6.14 поясняется принцип построения сумматора двух двоичных чисел на примере сложения четырехразрядного () и трехразрядного () чисел ( и  являются младшими разрядами). В табл. 6.15 приведен конкретный пример сложения двух чисел. Значения сигналов переноса С и разрядов d результирующего вектора вычисляются по формулам

,   ,   ,

,   ,   ,

,

,

.

Т а б л и ц а   6.14

                                                                                      Т а б л и ц а   6.15

          Для сложения младших разрядов  и  (при этом вычисляются значения младшего разряда результирующего вектора  и  сигнала переноса ) устанавливается НА (см. рис. 6.36).

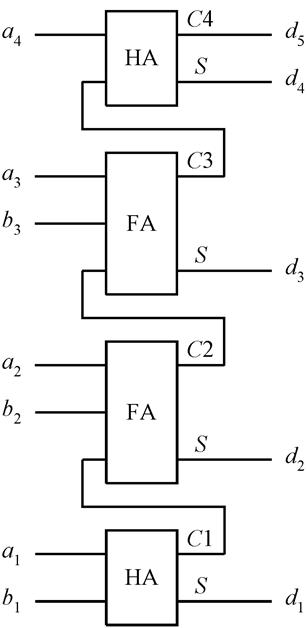
Рис.6.36. Сумматор двух двоичных чисел

Для вычисления значений сигналов , , а также ,  устанавливаются полные сумматоры FA, а значений сигналов ,  – полусумматор НА.

          Для уменьшения в схеме контроля про коду с суммированием избыточности, вносимой в блок  и СПТ, возможна организация контроля не по всем контрольным разрядам кода, а только по младшим разрядам. Если контроль осуществляется только по одному самому младшему разряду, то образуемая схема совпадает со схемой контроля по паритету. В этом случае подсчет числа единиц в векторе () (см. рис. 6.4) осуществляется по модулю 2. При контроле по всем контрольным разрядам кода подсчет числа единиц производится по модулю m + 1. С увеличением числа контролируемых разрядов увеличивается процент обнаруживаемых неисправностей, но и усложняются блоки  и СПТ. На практике используется контроль по двум младшим разрядам (подсчет числа единиц по модулю 4), при котором обнаруживается 95¸97% неисправностей по сравнению с контролем по полному коду.

6.6. Метод логического дополнения