Функциональное диагностирование дискретных систем, страница 17

Самодвойственные выходные сигналы  объединяются при помощи схемы сжатия (СЖ), на выходе которой формируется альтернативный сигнал . Последний контролируется ТСС. СЖ обладает следующими свойствами. Выходная функция  является самодвойственной, если все входные функции ,  ,…,   являются самодвойственными. Если какая-либо входная функция   искажается таким образом, что из самодвойственной превращается в несамодвойственную, то на тех  наборах, на которых нарушается свойство самодвойственности для функции , нарушается свойство самодвойственности и для выходной функции . Для любой одиночной константной неисправности СЖ существует хотя бы один набор значений входных самодвойственных функций , ,…,, на котором нарушается свойство самодвойственности выходной функции .

          Указанным свойством обладает элементарный модуль сжатия альтернативных сигналов, приведенный на рис. 6.49.

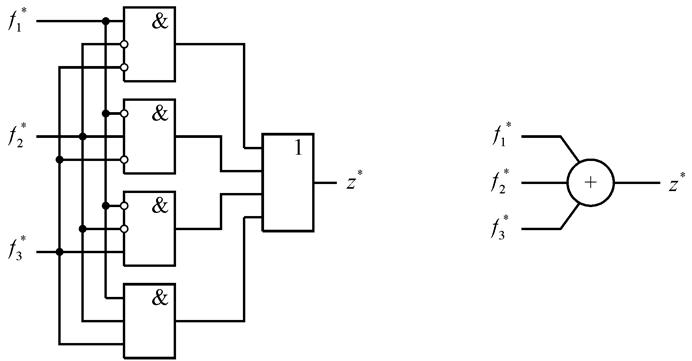
Рис.6.49. Структура (а) и условное обозначение (б) элементарного

                  модуля сжатия альтернативных сигналов

На выходе модуля реализуется функция контроля  нечетности. Схема сжатия для любого числа сигналов составляется путем последовательного соединения модулей. Если число сигналов четное, то на вход одного из модулей подается альтернативный сигнал  (см. рис. 6.50).

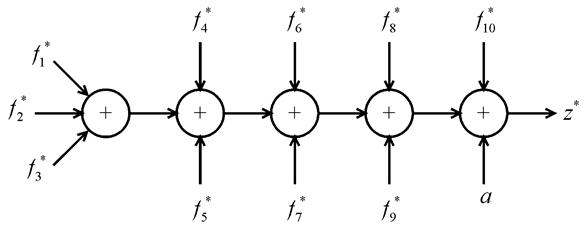
Рис.6.50. Схема сжатия десяти альтернативных сигналов

          На рис. 6.51 проиллюстрирован второй возможный принцип организации контроля схем на основе свойств самодвойственных функций.

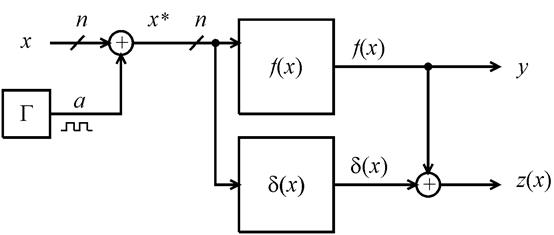
Рис.6.51. Обобщенная структура контроля схемы на основе

                  самодвойственного дополнения

В этом случае исходная схема  не преобразуется в самодвойственную схему, а дополнительный блок  вычисляет специальную контрольную функцию .

          Функция  называется самодвойственным дополнением функции , если

 = ,

где  – любая самодвойственная функция.

          Контроль самодвойственности функции  позволяет обнаруживать неисправности в блоках  и . Так как в качестве функции  может быть взята любая СД-функция (их число равно , -число  переменных  функции),  то возможно построить  схем блока . Среди них можно выбрать блок с минимальной сложностью. Эффективным является метод вычисления функции    ,    отраженный     в    табл.    6.18     для    функции     = . В данном случае существует 256 вариантов построения блока . Определим на первой половине наборов, для которых  = 0, значение  = 0. Тогда на этих наборах  =  = . Далее определим функцию  на второй половине наборов, для которых  = 1, как самодвойственную. И наконец, вычисляем значения функции  на второй половине наборов как  = . Минимизация этой функции дает результат  = .  В  таблице  приведены  еще три простых варианта  функции дополнения:  = ,  = ,  = .

          На рис. 6.52 приведена схема самодвойственного контроля рассмотренной функции.

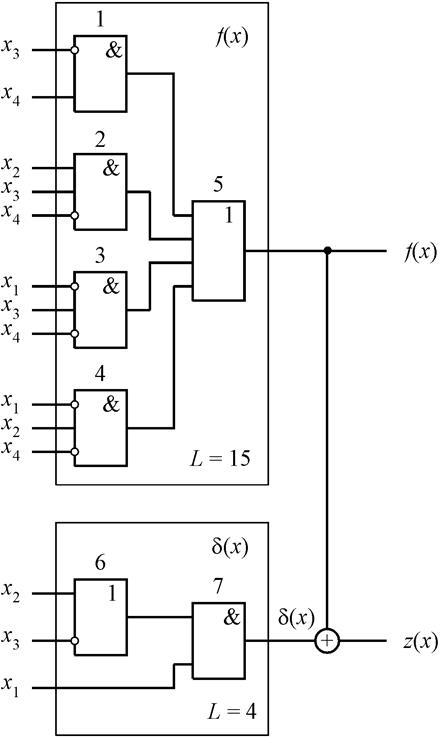
Рис.6.52. Схема самодвойственного контроля

Сложность дополнительного блока  = 4, что составляет 27% от сложности основного блока . На рис. 6.53 приведена временная диаграмма работы данной схемы при поступлении  на  ее вход последовательности наборов 0, 4, 11, 4, 4, 8

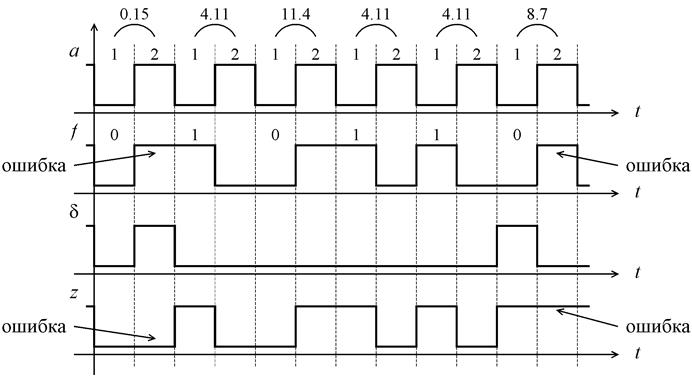
Рис.6.53. Временная диаграмма работы схемы самодвойственного

                  контроля

Т а б л и ц а   6.18