Особенности диагностирования систем непрерывного типа

Глава 8

ОСОБЕННОСТИ ДИАГНОСТИРОВАНИЯ

СИСТЕМ НЕПРЕРЫВНОГО ТИПА

8.1. Постановка задачи диагностирования

          Работа систем непрерывного типа характеризуется параметрами, которые изменяются в непрерывном множестве значений. На рис. 8.1 показано изменение во времени некоторого параметра (физической величины) , которая изменяется в пределах от верхнего  и нижнего  значений.

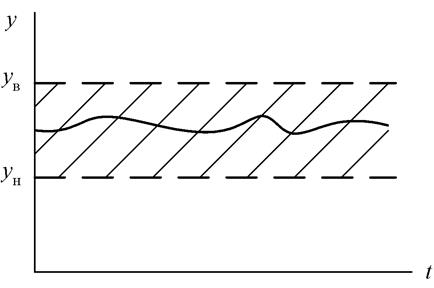
Рис.8.1. Изменение непрерывного диагностического сигнала

 Непрерывный параметр  называется диагностическим, если выход его значения за допустимые пределы  и  является признаком изменения состояния объекта.

          Таким образом, контроль непрерывного диагностического параметра заключается в его измерении и проверке выполнения неравенства

<  < .

Для целей диагностики непрерывную величину  можно описать дискретным признаком , который имеет два значения:

 = 1,  если <  <  (в норме);

 = 0,  в противном случае.

В более сложных случаях дискретному признаку присваиваются три значения:

 = , если   ;

 = , если  <  < ;

 = , если  >.

          В  общем   случае   непрерывная  система  характеризуется  некоторым множеством диагностических параметров . Каждому параметру  соответствует свой дискретный признак . Тогда при решении задач диагностики наряду с непрерывным описанием системы можно использовать дискретное описание. При этом состояние непрерывной системы описывается вектором

,

где  – признак, имеющий  разрядов.

          Если  m = 2, то вектор K является двоичным.

          Сформулируем теперь математическую постановку задачи диагноза непрерывной системы. Сама система может находиться в нескольких возможных состояниях (диагнозах) , которые считаются известными. Например – исправное, неисправное, работоспособное, неработоспособное, предотказное и др. Существуют два основных подхода к решению задачи диагноза – вероятностный и детерминированный.

          В  вероятностных  методах  считается, что система с некоторой вероятностью  находится  в  одном  из  случайных состояний . Известно множество диагностических параметров . Каждый параметр с определенной вероятностью характеризует состояние системы. Требуется построить алгоритм диагностирования (решающее правило), с помощью которого по данному множеству параметров определяется с достаточной достоверностью состояние системы .

          В детерминированных методах система характеризуется n-мерным вектором , который представляет собой точку в n-мерном пространстве признаков (параметров). Диагноз  соответствует некоторой области этого пространства. Требуется построить алгоритм диагностирования, который данный вектор K  относит к определенной области диагноза. Таким образом, задача состоит в разделении пространства признаков на области диагноза.

          Вероятностные методы являются более общими в том смысле, что могут оценивать достоверность того или иного диагноза и учитывать взаимозависимости между диагностическими параметрами. Но при этом эти методы требуют бóльшего объема информации. В детерминированных методах предполагается, что данный диагностический параметр с вероятностью равной единице соответствует допустимой норме или нет. Этот вывод делается в результате измерений. Вероятность данного (одного) диагноза считается также равной единице, вероятность остальных диагнозов равна нулю.

8.2. Метод Байеса

          Одним из наиболее простых и эффективных вероятностных методов технической диагностики при наличии достаточного объема статистических данных является метод, основанный на использовании обобщенной формулы Байеса.

          Пусть диагностируемая система может находиться в одном из состояний (диагнозах) , которые образуют полную группу несовместных событий. Это означает, что одновременно может быть поставлен только один диагноз . Из опыта эксплуатации подобных систем известны вероятности  нахождения системы в состоянии . Вероятность  называется априорной вероятностью диагноза. Так, если ранее наблюдалось  систем и у  систем имелось состояние , то

 = /.                                   (8.1)

          При этом

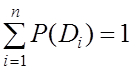.                                     (8.2)

          Пусть работа данной системы характеризуется диагностическим параметром . Событие (признак)  («выход параметра  за допустимые пределы») возникает при переходе системы в некоторые состояния  (при возникновении дефектов). Из опыта эксплуатации должны быть известны вероятности  появления признака  у системы в состоянии . Так, если ранее среди  систем, имеющих диагноз , признак  наблюдался у  систем, то

 = /.                                   (8.3)

Теперь задача диагноза может быть сформулирована следующим образом. У системы наблюдается признак , т.е. отклонился за допустимые пределы диагностический параметр . В каком состоянии  находится система с наибольшей вероятностью?

          Обозначим через  – вероятность того, что система находится в состоянии , если наблюдается признак . Эта вероятность называется апостериорной вероятностью диагноза. Ее определение и является целью диагноза. Вероятность того, что система находится в состоянии  и имеет признак  обозначим через . Тогда имеет место равенство