Особенности диагностирования систем непрерывного типа, страница 3

;

.

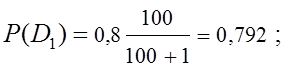
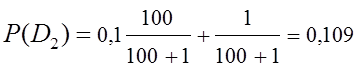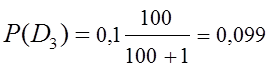Далее производится корректировка условных вероятностей признаков. Пусть у новой системы с диагнозом  выявлен разряд  признака . Тогда получаем новые значения условных вероятностей разрядов признака  при диагнозе по формулам:

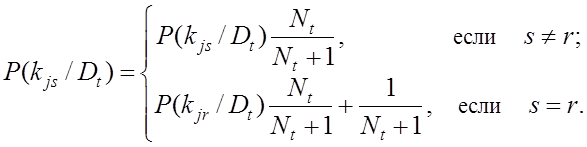    (8.14)

Пусть в нашем примере при диагнозе  выявлены следующие значения признаков: ,  и . Тогда по формулам (8.14) получаем новые значения условных вероятностей:

 ;

;

 ;

 ;

;

;

;

;

.

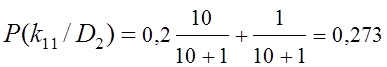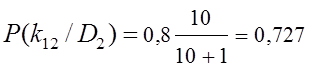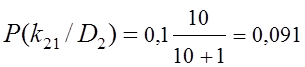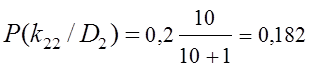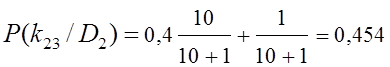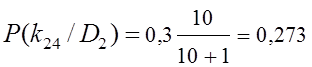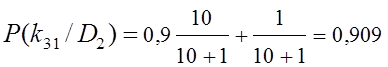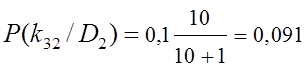          В табл. 8.2 приведена новая диагностическая таблица, которая будет использоваться при диагностировании следующей системы.

Т а б л и ц а   8.1

Диагноз	Признак
	0,6	0,3	0,1	0	0	0,2	0,8	0,6	0,4	0,8
	0,2	0,8	0	0,1	0,2	0,4	0,3	0,9	0,1	0,1
	0,5	0,1	0,4	0,3	0	0,2	0,5	0,5	0,5	0,1

Т а б л и ц а   8.2

Диагноз	Признак
	0,6	0,3	0,1	0	0	0,2	0,8	0,6	0,4	0,792
	0,273	0,727	0	0,091	0,182	0,454	0,273	0,909	0,091	0,109
	0,5	0,1	0,4	0,3	0	0,2	0,5	0,5	0,5	0,099

          Пример 8.2. Пусть для исследуемой системы А известна диагностическая таблица (табл. 8.3). Cистема А имеет три состояния: работоспособное состояние  и два состояния с неисправностями  и . Их априорные вероятности равны соответственно 0,9; 0,05; 0,05. При наблюдении за системой А проверяются два независимых параметра  и . Выход их за допустимые пределы составляет события  и . Признаки  и  являются двоичными. Поэтому в табл. 8.2 указывается только один разряд признака . Второй разряд (противоположное событие) будем обозначать как  и его вероятность  = 1 – .

          Определим апостериорные вероятности состояний системы, если существует признак  и отсутствует признак . Используя формулы (8.11) и (8.12) получаем:

 =

;

 =

;

 = .

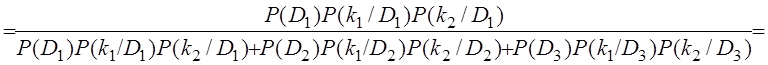
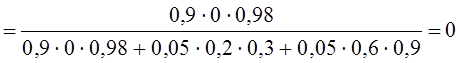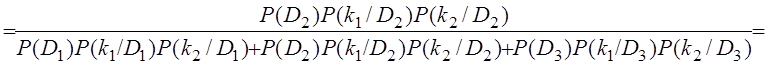
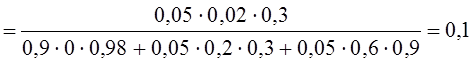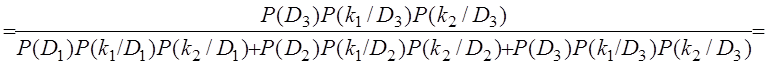
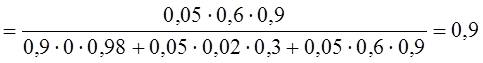          Так как признак  не наблюдается при работоспособном состоянии , то вероятность последнего равна 0. Наиболее вероятно (с вероятностью 0,9), что система А находится в состоянии . Результаты расчетов других апостериорных вероятностей состояний приведены в табл. 8.4.

          Таким образом, решающее правило, в соответствии с которым принимается решение о диагнозе в методе Байеса состоит в следующем: система с вектором признаков  относится к диагнозу  с наибольшей (апостериорной) вероятностью,

     Т а б л и ц а   8.3

	0	0,02	0,9
	0,2	0,7	0,05
	0,6	0,1	0,05

                                                                     Т а б л и ц а   8.4

	Вектор
	0,967	0	0,375	0
	0,013	0,1	0,583	0,7
	0,02	0,9	0,042	0,3

т.е. для диагноза  выполняется условие

 = max.                                  (8.15)

          Условие (8.15) может быть дополнено пороговым значением для вероятности диагноза: