Особенности диагностирования систем непрерывного типа, страница 2

 =  =,            (8.4)

где  – вероятность появления признака  независимо от состояния системы.

          Из формулы (8.4) следует формула Байеса

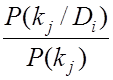 = .                            (8.5)

В формуле (8.5) величины  и  должны быть известны из статистических данных, полученных в процессе эксплуатации. Найдем величину . Событие  возникает вместе с одним из несовместных событий . Поэтому

 =  +  + … +  =

 = ++…+  (8.6)

или

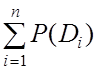
 =  .                           (8.7)

          Формула (8.7) является формулой полной вероятности события , происходящего вместе с полной группой независимых событий. С учетом (8.7) формула Байеса принимает вид:

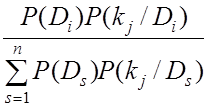 = .                         (8.8)

Из (8.8) следует, что

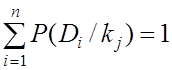,                                     (8.9)

то есть сумма апостериорных вероятностей диагноза для данного признака  равна 1.

          Для двух диагнозов  и  отношение апостериорных вероятностей

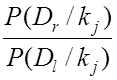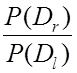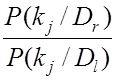 =  × .                      (8.10)

Это отношение пропорционально отношению априорных вероятностей и отношению условных вероятностей появления признака  в состояниях  и .

          Пример 8.1.  Известны   интенсивность  отказов  системы  А   = 1,5 × 10^–4 1/час. Контроль за работой системы осуществляется путем измерения параметра . Из опыта эксплуатации известно, что при выходе за допустимые пределы параметра  (при наличии признака ) система выходит из строя в 5% случаев. Определить вероятность работоспособного состояния системы А через 1000 часов при появлении признака .

          Обозначим работоспособное состояние системы как ,  – неработоспособное состояние. Вероятности  = 0,05;  = 0,95.  Вероятность   =  =   =  = 0,85. По формуле (8.8) имеем

 =

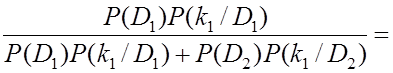
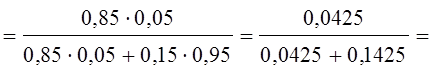
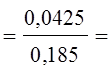 0,23.

Таким образом вероятность работоспособного состояния системы при появлении признака  снижается с 0,85 до 0,23.

          Обобщенная формула Байеса применяется, если диагностируемая система характеризуется множеством параметров  и в результате измерений становится известен вектор признаков . Здесь знак * означает конкретную реализацию признака . Тогда формула (8.8) принимает вид (обобщенная формула Байеса):

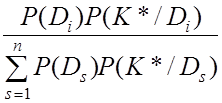 = ,                     (8.11)

где  – апостериорная вероятность диагноза после того, как стали известны результаты измерений по вектору признаков K.

          При условии независимости диагностических признаков величина  рассчитывается по формуле:

 =  … .    (8.12)

          При использовании метода Байеса составляется диагностическая таблица (табл. 8.1) на основе статистического материала. В ней для каждого диагноза   указывается значение априорной вероятности этого диагноза (в столбце ) и вероятностей появления разрядов признаков (в столбцах ).

          Табл. 8.1 составлена для системы А, имеющей три состояния   . При этом

.

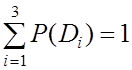Наибольшую вероятность имеет состояние  ( = 0,8). Система А характеризуется тремя признаками ,  и , которые имеют соответственно 3, 4 и 2 разряда. Например, в состоянии  разряды  и  признака  не наблюдаются (вероятности их появления равны нулю), разряд  наблюдается с вероятностью 0,2, а разряд  – с вероятностью 0,8. Сумма вероятностей всех возможных реализаций признака для данного диагноза  равна единице.

          В процессе эксплуатации и диагностики однотипных систем производится корректировка диагностической таблицы. При этом для обработки результатов необходимо хранить не только данные таблицы 8.1, но и следующие данные:  – общее число систем, обследованных при составлении диагностической таблицы;  – число систем с диагнозом . Пусть, например, для табл. 8.1 имеем:  = 100,  = 80,  = 10,  = 10.

          Если обследуется новая система и устанавливается ее диагноз  (), то производится корректировка прежних априорных вероятностей диагнозов по формулам:

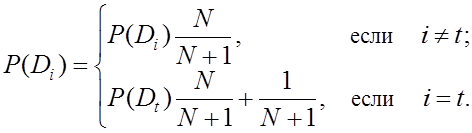              (8.13)

Пусть, например, при обследовании новой системы в нашем примере (табл. 8.1) был установлен диагноз . Тогда получаем новые значения априорных вероятностей диагнозов: