1.7. Нагрузка
Нагрузка – это потребители электрической энергии, преобразующие ее в другие виды (тепловую, механическую, световую и т.д.). Обычно в расчетах рассматриваются не отдельные потребители, а ее узлы – группы нагрузок, присоединенных к шинам подстанции.
Представление нагрузки в расчетах переходных процессов в схемах электроснабжения определяется целью расчета и его точности. Нагрузку можно представить в виде постоянных активного и индуктивного сопротивлений в упрощенных расчетах статической и динамической устойчивости при условии сохранения устойчивости самой нагрузки.
Полное сопротивление нагрузки для последовательно соединенных активного и реактивного сопротивлений определяется по формуле:
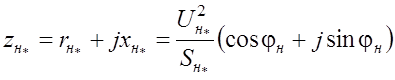 , о.е., (1.20)
, о.е., (1.20)
где ![]() – полная мощность нагрузки в
относительных единицах;
– полная мощность нагрузки в
относительных единицах;
![]() – коэффициент мощности
нагрузки, о.е.;
– коэффициент мощности
нагрузки, о.е.;
![]() – напряжение в точке
подключения нагрузки, о.е.
– напряжение в точке
подключения нагрузки, о.е.
При представлении нагрузки параллельно соединенными активным и реактивным сопротивлениями их значения определяется по формулам:
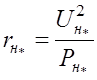 , о.е., (1.21)
, о.е., (1.21)
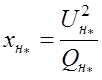 , о.е. (1.22)
, о.е. (1.22)
Нагрузку можно
представить статическими характеристиками по напряжению (![]() ,
, ![]() ) и по
частоте (
) и по
частоте (![]() ,
, ![]() ) в
расчетах устойчивости нагрузки или системы в послеаварийном режиме.
) в
расчетах устойчивости нагрузки или системы в послеаварийном режиме.
Статические характеристики нагрузки по напряжению могут быть получены: 1) из натурного эксперимента; 2) из расчета с детальным учетом состава нагрузки; 3) на основании статистических данных. Часто при проведении расчетов переходных процессов трудно определить состав нагрузок и их достоверные параметры. В этом случае используются типовые характеристики комплексной нагрузки. При отсутствии конкретных данных рекомендуется принимать следующие характеристики комплексной нагрузки:
– для активной нагрузки в среднем
![]() ,
о.е. (1.23)
,
о.е. (1.23)
с диапазоном изменения
![]() , о.е., (1.24)
, о.е., (1.24)
![]() , о.е.; (1.25)
, о.е.; (1.25)
– для реактивной нагрузки на стороне 110…220 кВ в среднем
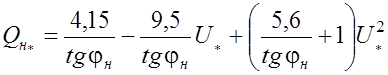 ,
о.е. (1.26)
,
о.е. (1.26)
с диапазоном изменения
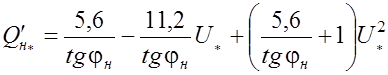 ,
о.е., (1.27)
,
о.е., (1.27)
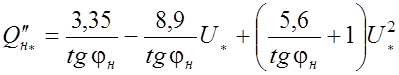 ,
о.е. (1.28)
,
о.е. (1.28)
Пример 1. Рассмотрим схему электропередачи, в которой генератор работает через трансформатор и двухцепную линию электропередачи на шины приемной системы бесконечной мощности. Напряжение приемной станции U можно считать неизменной по абсолютному значению и фазе при любых условиях работы электропередачи.
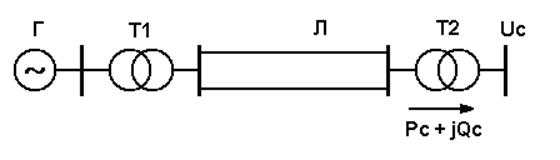
Исходные данные:
– генератор: Pном = 100 МВт; ![]() =0,8;
=0,8; ![]() =0,278;
Uном = 10,5 кВ;
=0,278;
Uном = 10,5 кВ; ![]() =1,907;
=1,907; ![]() = 6,7 с;
= 6,7 с;
– трансформатор Т1: Sном = 160 МВА; Uном = 11/230 кВ; Uk = 11 %;
– линия: ![]() = 0,4 Ом/км; L = 300
км;
= 0,4 Ом/км; L = 300
км;
– трансформатор Т2: Sном = 200 МВА; Uном = 230/110 кВ; Uk = 11 %;
– передаваемая мощность Рс = 80 МВт и Qс = 30 Мвар.
Определить все сопротивления схемы замещения и ЭДС генератора в случае:
– при отсутствии автоматического регулятора возбуждения;
– при АРВ пропорционального типа;
– при АРВ сильного действия типа.
Расчет будем проводить, используя приближенное приведение элементов схемы замещения в относительных единицах.
Принимаем базисные условия:
Sб = 80 МВт, Uб = 115 кВ.
Напряжение системы в относительных единицах равно:
Uc* = 115/115 = 1.
Передаваемая активная мощность в относительных единицах равна:
Pc* = 80/80 = 1.
Передаваемая реактивная мощность в относительных единицах равна:
Qc* = 30/80 = 0,375.
Сопротивление генератора в относительных единицах без учета АРВ:
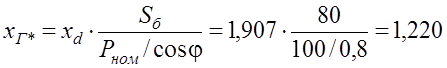 .
.
Сопротивление трансформатора Т1 в относительных единицах равно:
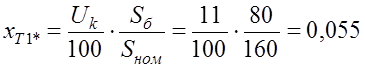 .
.
Сопротивление линии в относительных единицах равно:
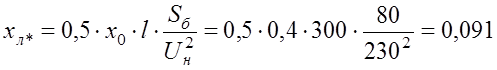 .
.
Сопротивление трансформатора Т2 в относительных единицах равно:
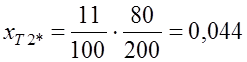 .
.
Результирующее сопротивление системы без учета АРВ:
![]() .
.
Синхронная ЭДС генератора:
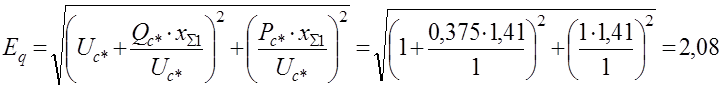 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.