














Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
«Комсомольский-на-Амуре государственный технический университет»
Кафедра «Механика и анализ конструкций и процессов»
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛКАХ И ПЛОСКИХ РАМАХ
Методические указания по курсу «Строительная механика»
Комсомольск-на-Амуре 2009
![]()
Определение перемещений в статически определимых балках и плоских рамах: Методические указания по курсу «Строительная механика» / Сост.: В.С. Симонов, С.В. Макаренко. – Комсомольск-на-Амуре: ГОУ ВПО «КнАГТУ», 2009. – 19 с.
Методические указания содержат рекомендации по реализации метода определения перемещений в названных системах с помощью интегралов Мора.
Приведены примеры определения перемещений в составных статически определимых балке и раме. Решения примеров сопровождаются необходимыми рисунками и комментариями.
Методические указания предназначены для студентов всех форм обучения, изучающих курс «Строительная механика».
Печатается по постановлению редакционно-издательского совета ГОУ ВПО «Комсомольский-на-Амуре государственный технический университет».
Согласовано с отделом МК
Рецензент Г.С. Лейзерович
ВВЕДЕНИЕ
Определение перемещений в стержневых статически определимых системах является одной из основных задач строительной механики. Наиболее просто линейные и угловые перемещения, возникающие в любой стержневой системе от внешней нагрузки, могут быть найдены с помощью интегралов Мора.
Изучению основ универсального метода определения перемещений с помощью интегралов Мора и приобретению практических навыков в решении конкретных задач способствует выполнение соответствующей контрольной работы. В этой работе предусмотрено определение линейных и угловых перемещений в плоских статически определимых стержневых системах (балках и рамах) по формуле перемещений (интегралу Мора) с использованием правила Верещагина или готовых формул перемножения эпюр.
1. Краткие общие методические указания
В стержневых системах рассматриваемого типа перемещения обусловлены, главным образом, деформацией изгиба, поэтому в формуле перемещений учитываются интегралы Мора только одного вида
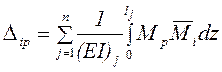 (1)
(1)
Здесь ![]() – линейное (или угловое)
перемещение от заданной нагрузки в i-м
направлении;
– линейное (или угловое)
перемещение от заданной нагрузки в i-м
направлении;
j – номер участка стержневой системы;
n – число участков стержневой системы;
(EI)j– изгибная жесткость j-го участка;
lj – длина j-го участка;
MP=MP(z) – изгибающий момент на j–м участке от заданной нагрузки;
![]() – изгибающий момент на j–м участке от единичной силы
– изгибающий момент на j–м участке от единичной силы ![]() (при вычислении линейного перемещения) или
(при вычислении линейного перемещения) или
![]() (при вычислении угла поворота),
приложенных в исследуемом сечении и заданном направлении.
(при вычислении угла поворота),
приложенных в исследуемом сечении и заданном направлении.
Вычисление интегралов Мора (1) для стержневых систем, составленных из прямолинейных стержней, существенно упрощается и может быть выполнено по правилу Верещагина или по готовым формулам.
Правило Верещагина предполагает графическое
изображение выражений MР(z) и ![]() , т.е. построение эпюр изгибающих
моментов так называемых грузового состояния MР и единичного состояния
, т.е. построение эпюр изгибающих
моментов так называемых грузового состояния MР и единичного состояния ![]() .
В соответствии с этим правилом
.
В соответствии с этим правилом
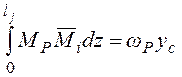 , (2)
, (2)
где ωP – площадь грузовой эпюры Mp на j– м участке;
yc – ордината эпюры ![]() под
центром тяжести площади ωP.
под
центром тяжести площади ωP.
Обратим внимание на то, что в пределах площади ωP эпюра ![]() должна
быть линейной и непрерывной, т.е. не должна иметь изломов, разрывов («скачков»).
Требование линейности эпюры
должна
быть линейной и непрерывной, т.е. не должна иметь изломов, разрывов («скачков»).
Требование линейности эпюры ![]() для балок и рам всегда
удовлетворяется, а требование непрерывности достигается соответствующим разбиением
стержневой системы на участки.
для балок и рам всегда
удовлетворяется, а требование непрерывности достигается соответствующим разбиением
стержневой системы на участки.
С целью упрощения расчётов эпюра MР (площадь ωP) расчленяется на простейшие геометрические фигуры, для каждой из которых известны положение центра тяжести и формула для вычисления площади. В этом случае, учитывая (2), правило Верещагина представляется в виде:
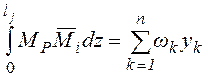 . (3)
. (3)
Здесь k– номер простой фигуры эпюры МР;
n – число простых фигур;
![]() –
площадь простой фигуры эпюры МР;
–
площадь простой фигуры эпюры МР;
yk – ордината единичной эпюры ![]() под
центром тяжести площади
под
центром тяжести площади ![]() .
.
Произведение ωk·ykбудет положительным, если ![]() и yk одного знака, и отрицательным,
если
и yk одного знака, и отрицательным,
если ![]() и
yk противоположных знаков.
и
yk противоположных знаков.
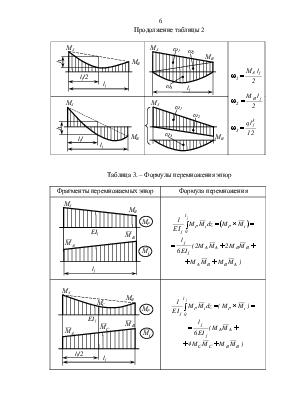
Грузовая эпюра MР любого очертания (при q=const) может быть расчленена на простые фигуры трёх видов, представленных таблице 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.