Определение перемещений в статически определимых балках и плоских рамах: Методические указания по курсу «Строительная механика», страница 2

В учебной литературе приводятся и две другие простые геометрические фигуры для участков с q=const, но для их выделения необходимо быть абсолютно уверенным в правильности изображения эпюры М_Р на этих участках.

Приёмы расчленения наиболее часто встречающихся фрагментов эпюр М_Р с использованием приведенных выше простых фигур представлены в таблице 2.

Интеграл Мора вычисляют и по готовым формулам, которые можно получить из правила Верещагина или из приближенного способа вычисления интеграла Мора при произвольном виде выражений М_Р(z) и  по методу Симпсона, который для рассматриваемых систем в случае q = const даёт точный результат.

Готовые формулы перемножения эпюр  и  приведены в таблице 3.

Таблица 1. – Простые геометрические фигуры

Таблица 2. – Расчленение эпюры M_p на простые фигуры

Продолжение таблицы 2

Таблица 3. – Формулы перемножения эпюр

Фрагменты перемножаемых эпюр	Формула перемножения
МР   lj   EIj   МВ   МА
МР   МВ   lj/2   МC   lj   EIj   МА

Изгибающие моменты М_С и вычисляются по формулам

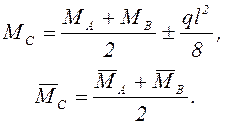                                           (4)

Знак при ql²/8 берётся в соответствии с направлением нагрузки q. В формулах перемножения эпюр, приведенных в таблице 3, и в (4) необходимо учитывать знаки ,, в случае перемножения так называемых «перекрученных» эпюр М_Р и , что иллюстрируется в примерах вычисления некоторых перемещений в балке и раме по готовым формулам.

2. ПРИМЕР ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ В БАЛКЕ

Определить прогибы незакреплённых сечений 1, 2, 3, 5, 6 и изобразить изогнутую ось балки, расчётная схема которой приведена на рисунке 1.

Рисунок 1 – Расчётная схема балки

Решение задачи выполняем в такой последовательности.

2.1. Строим эпюру изгибающих моментов от заданной нагрузки – так называемую грузовую эпюру М_Р.

Определяем опорные реакции, используя этажную схему балки (рисунок 2), в которой выделены основная 0–2 и вспомогательная 2– 6 части.

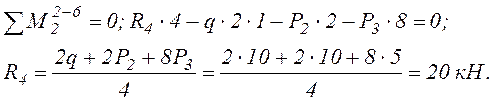
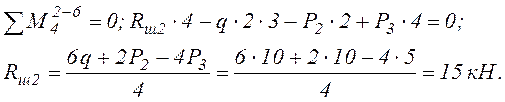
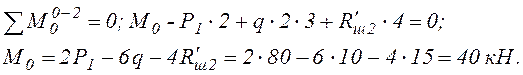
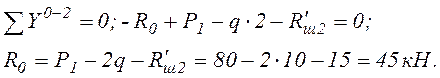
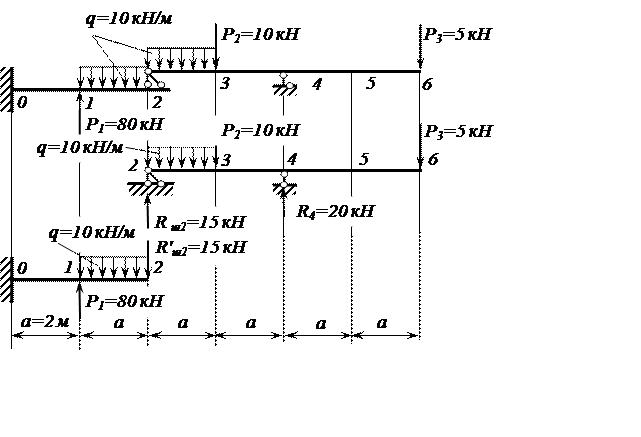
Рисунок 2. – Поэтажная схема грузового состояния балки

Вычисляем значения изгибающих моментов в характерных сечениях (на границах участков):

а) основная балка 0 – 2;

М_0-1 = М₀ = 40 кН·м (растянутые волокна внизу);

М_1-0 = М_1-2 = М₀ –R₀ ·2 = 40 –45·2 = -50 кН·м (растянутые волокна вверху);

М_2-1 = 0  (сечение 2 – шарнир);

б) вспомогательная балка 2 – 6;

М_2-3 = 0  (сечение 2 – шарнир);

М_3-2 = М_3-4 =R_ш2 ·2 – q·2·1= 15·2 – 10·2·1 = 10 кН·м (растянутые волокна внизу);