Определение перемещений в статически определимых балках и плоских рамах: Методические указания по курсу «Строительная механика», страница 4

Участок стойки AL.

M_{A – L} =0; M_{L – A} =R_AХ··2 = 5,333·2 =10,67 кН·м.

Участок стойки LK.

M_{L – K} = M_{L – A} =R_AХ ·2 = 5,333·2 =10,67 кН·м;

M_{K – L} =R _AХ ·6 – P·4 = 5,333·6 – 20·4 = - 48 кН·м.

Положительные значения M_L–K = M_L–Aоткладываем на эпюре М_Р справа от оси стойки, т.к. принятая в выражении изгибающего момента положительной сила R_AХ вызывает при изгибе стойки растяжение волокон справа. Отрицательное значение M_{K – L} откладываем в этом случае слева.

Наклонный участок КС.

M_{С – K} = 0 (в шарнире М=0);

M_{K – С} =R_AХ ·6 – P·4 = M_{K – L}= - 48 кН·м.

Отрицательное значение следует отложить вверх (снаружи рамы), т.к. R_BХ, принятая положительной, при изгибе ригеля вызывает растяжение нижних волокон и вниз откладывалось бы положительное значение М_К–С.

Стойка BD.

M_{B – D}=R_BX··3 = 14,667·3 = 44 кН·м.

Значение М_В–D откладываем справа от оси стойки.

Ригель СD.

M_{С – D} = 0; .M_D–C = R_BХ ·3 = 14,667·3 = 44 кН·м.

Значение  M_D–Cоткладываем вверх от оси ригеля.

Значение изгибающего момента посередине ригеля CD по (4)

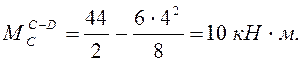
По значениям изгибающих моментов в характерных сечениях строим эпюру М_Р с учётом направления распределенной внешней нагрузки (рис. 8).

Для перемножения эпюр по правилу Верещагина представим эпюру М_Р в расчленённом виде (рисунок 9).

Рисунок 8.– Грузовая эпюра М_Р

Рисунок 9. – Грузовая эпюра М_Р в расчленённом виде

3.2. Аналогично строим единичные эпюры  и , «нагружая» раму поочерёдно единичной силой  и единичным моментом .

Учитывая простоту каждого из единичных состояний, расчёты здесь не приводим, а сами эпюры изобразим на расчётных схемах рамы (рисунки 10, 11).

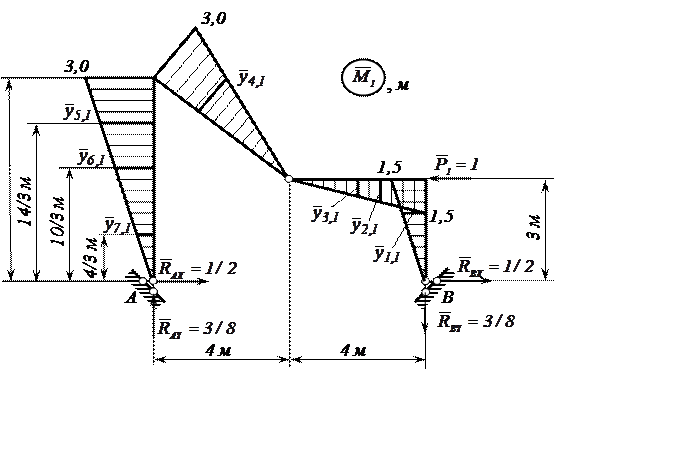
Рисунок 10. – Первое единичное состояние

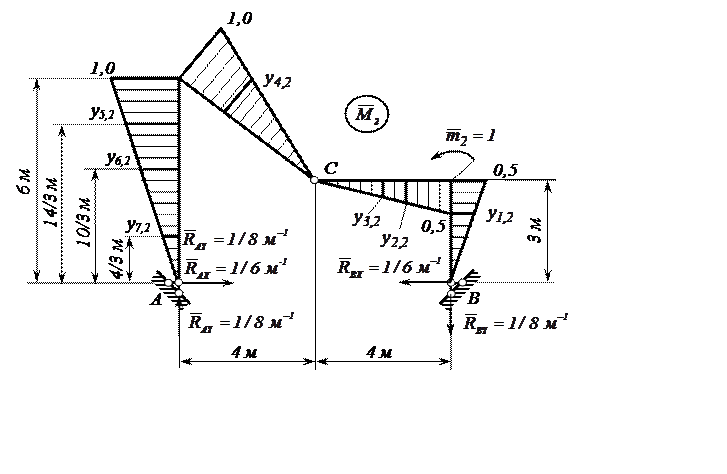
Рисунок 11. – Второе единичное состояние

Значения единичных эпюр под центрами тяжести площадей грузовой эпюры можно вычислить из подобия треугольников, но надёжнее, особенно для стойки АК, через реакции опорных связей, например,

на эпюре

;

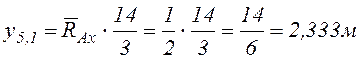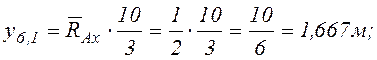
на эпюре

.

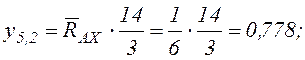
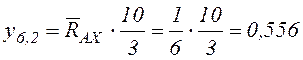3.3. Вычисляем горизонтальные перемещения  и угол поворота  узла D, перемножая эпюры по правилу Верещагина (3).

Значения площадей грузовой эпюры и соответствующие ординаты единичных эпюр сведём в таблицу 5.

Таблица 5. – Значения площадей эпюры М_Р и ординат эпюр

№ площади, j	, кН·м2	Ординаты эпюр под центрами тяжести составляющих площадей эпюры МР
		Эп. , м	Эп.
1	66,00	1,0	0,333
2	88,00	1,0	0,333
3	32,00	0,75	0,25
4	120,00	2,0	0,667
5	96,00	2,333	0,778
6	21,34	1,667	0,556
7	10,67	0,667	0,222

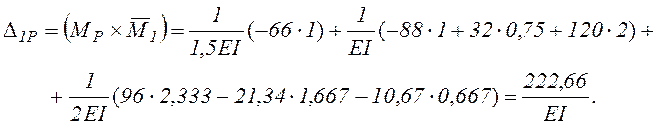
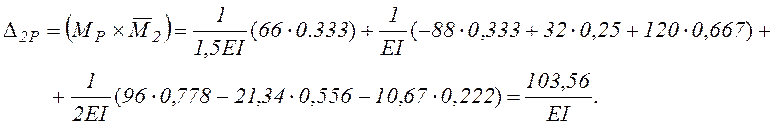
3.4. Вычисляем те же перемещения, перемножая эпюры по готовым формулам

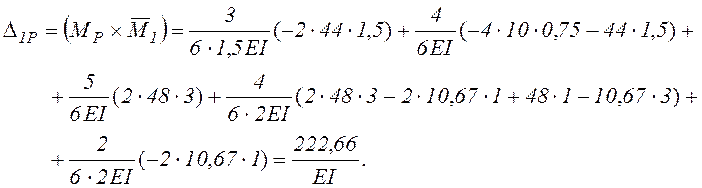
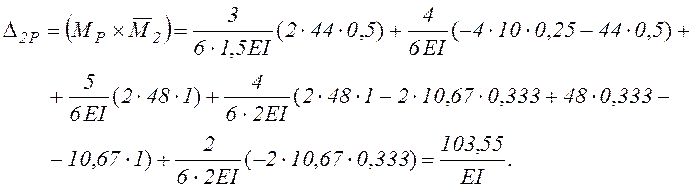
Таким образом, узел D смещается в направлении , т.е. влево, и поворачивается в направлении , т.е. против хода часовой стрелки.

Заметим, что числитель в линейном перемещении  измеряется в кН·м³, а в угловом  – в кН·м².

ЗАКЛЮЧЕНИЕ

Определение перемещений в статически определимых системах является, как отмечалось, одной из основных задач строительной механики, но не только как самостоятельная задача расчёта строительных конструкций на жёсткость.

Умение определять линейные и угловые перемещения необходимо для успешного изучения и реализации методов расчёта статически неопределимых стержневых систем методом сил. Так, например, формирование системы канонических уравнений метода сил предполагает определение перемещений грузового и единичных состояний основной системы, как промежуточный этап решения задачи.

Деформационная проверка правильности раскрытия статической неопределимости так же заключается в определении перемещений основной системы метода сил в направлениях «лишних» связей.

Следовательно, изучению метода определения перемещений с помощью интегралов Мора и приобретению практических навыков решения конкретных задач необходимо уделить особое внимание.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Дарков, А.В. Строительная механика: учебник для вузов / А.В. Дарков,

Н.Н. Шапошников. – 9-е изд., испр. – СПб.: Лань, 2004. – 655 с.

2. Саргсян, А.Е. Строительная механика. Механика инженерных конструкций: учебник для вузов / А.Е. Саргсян. – М.: Высш. школа, 2004. – 403 с.

3. Руководство к практическим занятиям по курсу строительной механики: Статика стержневых систем. Учеб. пособие для строит. спец. вузов / Под общ. ред. Г.К. Клейна. – 4-е изд., перераб. и доп. – М.: Высшая школа, 1980. – 384 с.