Определение перемещений в статически определимых балках и плоских рамах: Методические указания по курсу «Строительная механика», страница 3

М_4-3 = М_4-5 = Р₃·4 = 5·4 = 20 кН·м (растянутые волокна вверху);

М_5-4 = М_5-6 = Р₃·2 = 5·2 = 10 кН·м (растянутые волокна вверху).

По значениям в характерных сечениях строим эпюру М_Р с учётом направления распределенной нагрузки.

На участках 1-2 и 2-3 находим дополнительно значения М_Р посередине, необходимые при перемножении эпюр по готовым формулам, используя (4).

; ; .

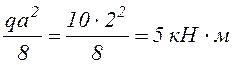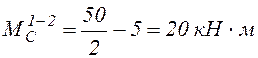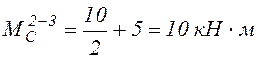Значения изгибающих моментов на эпюре М_Р откладываем со стороны растянутых волокон балки, при этом знаки изгибающих моментов принято не указывать (рисунок 3).

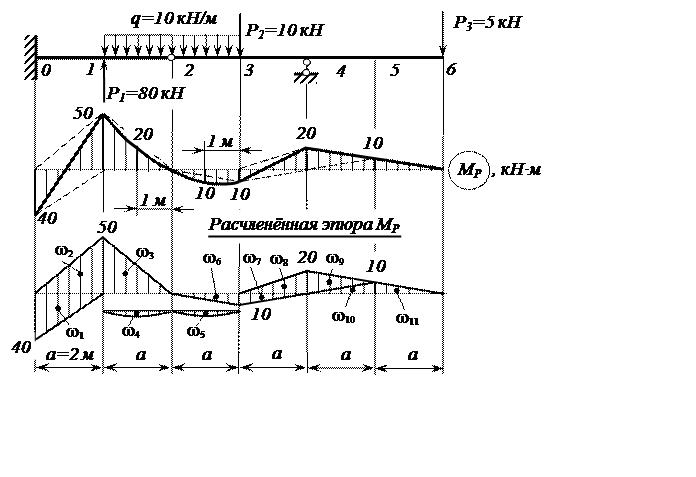
Рисунок 3. – Грузовая эпюра изгибающих моментов М_Р

2.2. Для вычисления прогибов в сечениях 1, 2, 3, 5, 6 строим эпюры изгибающих моментов так называемых единичных состояний, загружая балку поочерёдно единичными силами , приложенными в соответствующих сечениях (рисунок 4).

2.3. Определяем прогибы балки в заданных сечениях, «перемножая» эпюру М_Р на соответствующие единичные эпюры .

2.3.2. Для перемножения эпюр по правилу Верещагина (3) представим грузовую эпюру М_Р в виде суммы простых площадей. Учтём при этом, что в пределах каждой площади все единичные эпюры должны быть непрерывными, а жёсткость EI = const.

Расчленённую эпюру М_Р и единичные эпюры  изобразим на одном рисунке (рисунок 5).

Значения площадей грузовой эпюры и соответствующие им значения единичных эпюр сведем в таблицу 4.

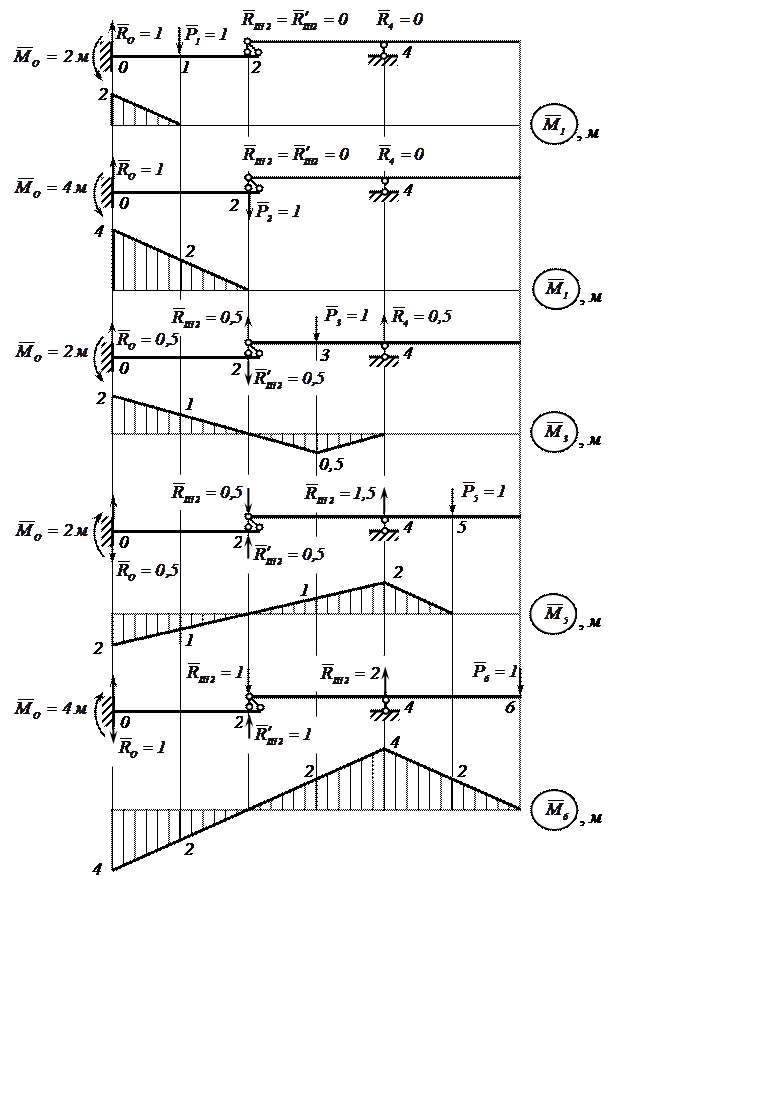
Рисунок 4. – Единичные состояния балки и единичные эпюры

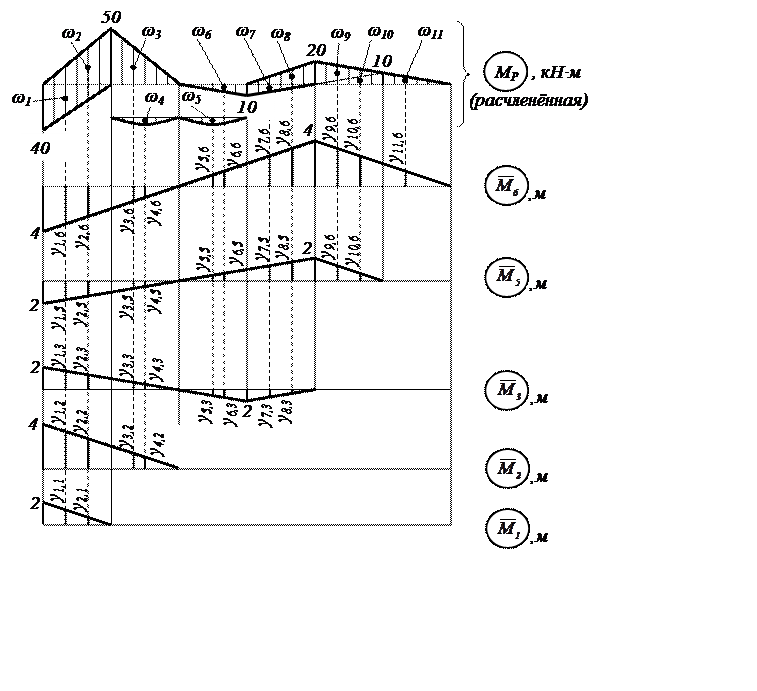
Рисунок 5. – Грузовая и единичные эпюры изгибающих моментов,

подготовленные к перемножению эпюр по правилу Верещагина

Таблица 4. – Значения площадей эпюры М_Р и ординат эпюр

№ площади – j	, кН·м2	Ординаты единичных эпюр  под центрами тяжести составляющих площадей – yj,i , м
		Эп.	Эп.	Эп.	Эп.	Эп.
1	40	4/3	10/3	5/3	5/3	10/3
2	50	2/3	8/3	4/3	4/3	8/3
3	50		4/3	2/3	2/3	4/3
4	20/3		1	1/2	1/2	1
5	20/3			1/2	1/2	1
6	10			2/3	2/3	4/3
7	10			2/3	4/3	8/3
8	20			1/3	5/3	10/3
9	20				4/3	10/3
10	10				2/3	8/3
11	10					4/3

Определяем вертикальные перемещения Δ_1Р, Δ_2Р, Δ_3Р, Δ_5Р, Δ_6Р, перемножая соответствующие эпюры по правилу Верещагина.

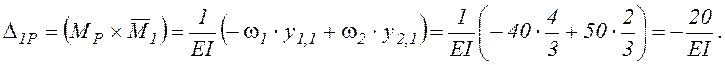
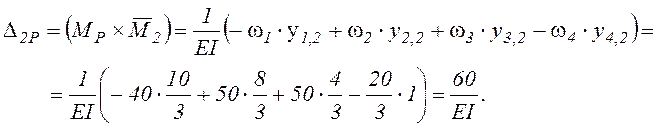
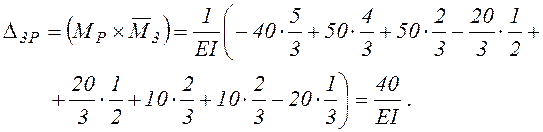
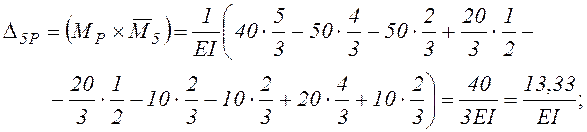
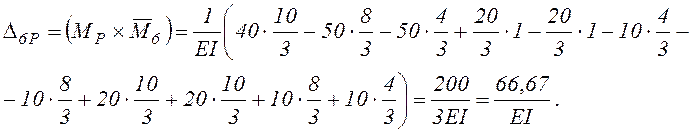
2.3.2. Использование готовых формул перемножения эпюр покажем на примере вычисления Δ_5Р (см. таблицу 3).

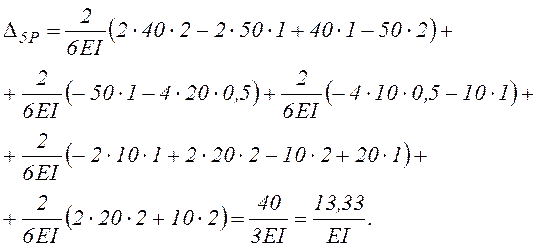
Заметим, что числитель в линейных перемещениях измеряется в кН·м³, что необходимо учитывать при вычислении значений прогибов для конкретных поперечных сечений балки. Например, для стальной балки двутаврового сечения № 24 (I_x=3460 cм⁴, Е=2·10⁵ МПа=2·10⁴кН/см²) значение прогиба сечения 6 (максимальное по модулю):

.

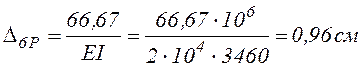Здесь 66,67 кН·м³ = 66,67·10⁶ кН·см³.

По значениям вертикальных перемещений (прогибов) отдельных сечений изображаем изогнутую ось балки, согласуя характер изгиба с грузовой эпюрой изгибающих моментов. Согласование заключается в удовлетворении закона Гука при изгибе

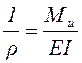,                                                                      (5)

т.е. кривизна (форма и «степень» искривления изогнутой оси) определяются значением изгибающего момента и тем, с какой стороны на эпюре М_Р это значение отложено. При смене знака изгибающего момента изменяется и знак кривизны.

Для наглядности удовлетворения условия (5) изображение изогнутой (упругой) оси балки поместим под эпюрой изгибающих моментов М_Р (рисунок 6).

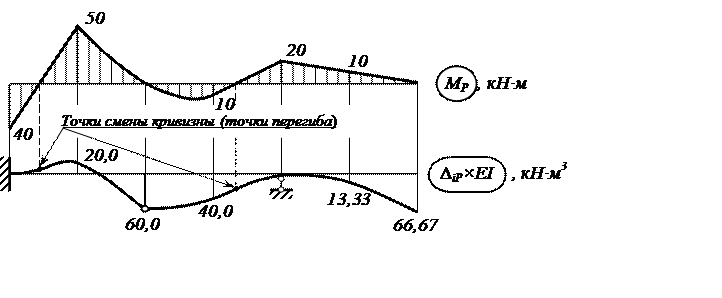
Рисунок 6. – Согласование изогнутой оси балки с эпюрой изгибающих

моментов

3. ПРИМЕР ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ В РАМЕ

Определить горизонтальное перемещение и угол поворота узла D рамы, расчётная схема которой приведена на рисунке 7.

Рисунок 7. – Расчётная схема рамы

Решение выполняется в той же последовательности, что и в предыдущем примере.

1. Строим эпюру изгибающих моментов М_Р, предварительно определив реакции опорных связей (реакции опор).

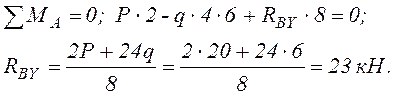
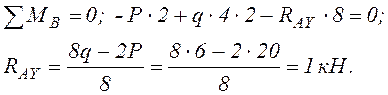
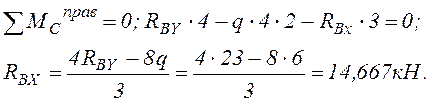
Проверим найденные реакции:

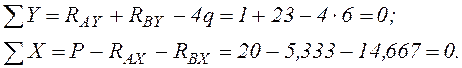
Эпюру изгибающих моментов М_Р строим со стороны растянутых волокон по значениям в характерных сечениях рамы.