Расчет статически неопределимых плоских рам методом сил: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика"

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

«Комсомольский-на-Амуре государственный технический университет»

Кафедра «Механика и анализ конструкций и процессов»

РАСЧЁТ СТАТИЧЕСКИ НЕПРЕДЕЛИМЫХ ПЛОСКИХ РАМ

МЕТОДОМ СИЛ

Методические указания к выполнению контрольной и расчётно-проектировочной работы по строительной механике

Комсомольск-на-Амуре 2009

УДК 624.04

 

Расчёт статически неопределимых плоских рам методом сил: Методические указания по курсу «Строительная механика» / Сост. В.С. Симонов, Г.С. Лейзерович – Комсомольск-на-Амуре: ГОУВПО «Комсомольский-на-Амуре государственный технический университет», 2009. – 17 с.

Методические указания содержат рекомендации по реализации метода сил для раскрытия статической неопределимости плоских рам.

Приведен пример расчёта дважды статически неопределимой плоской рамы. Решение примера сопровождается необходимыми рисунками и комментариями.

Методические указания предназначены для студентов заочной и дневной форм обучения, изучающих курс «Строительная механика».

Печатается по постановлению редакционно-издательского совета ГОУВПО «Комсомольский-на-Амуре государственный технический университет».

Согласовано с отделом стандартизации.

Рецензент Ю.Н. Чудинов

1. ОБЩИЕ ПОЛОЖЕНИЯ МЕТОДА СИЛ. ПРИМЕНЕНИЕ МЕТОДА СИЛ

К РАСЧЁТУ ПЛОСКИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ РАМ

Метод сил является одним из универсальных (классических) методов расчёта статически неопределимых стержневых систем. Его название объясняется тем, что в качестве неизвестных принимаются усилия (силы или моменты сил) в так называемых «лишних связях».

«Лишние» связи – это связи сверх кинематически необходимых, и их число в плоской стержневой системе определяется по одной из формул:

а)                                                                                        (1.1)

где: n – число «лишних» связей;

К – число замкнутых контуров, образуемых стержнями рамы, включая основание («землю»);

Ш – число простых шарниров (приведенное число) в контурах.

б)                                                                  (1.2)

где: w – степень свободы стержневой системы

С_оп – число опорных связей;

Ш – число простых шарниров, соединяющих между собой «диски»;

D – число простых стержневых дисков, не содержащих замкнутых контуров (основание как диск не учитывается).

Замечание. Понятия о кинематическом анализе стержневых систем («диск», «простые шарниры», «степень свободы», рассматривались в первой части курса «Строительная механика»).

Степень статической неопределимости n равна числу «лишних» связей.

В методе сил используют понятия: заданная система (ЗС), основная система (ОС) и эквивалентная система (ЭС).

Заданная система – расчётная схема стержневой системы, подлежащая расчёту (определение внутренних усилий N, Q, M и перемещений).

Основная система – получается из заданной системы путём устранения «лишних» связей. Заметим, что основная система не «несёт» на себе никаких нагрузок (схема в «обнажённом» виде).

Эквивалентная система – это основная система, загруженная заданной нагрузкой и предполагаемыми направлениями усилий в устранённых «лишних» связях

Основными приёмами устранения «лишних» связей при выборе варианта основной системы метода сил могут быть:

а) полное рассечение стержня – устраняет 3 внутренних связи: угловую и две линейные связи;

б) разъединение отдельных частей рамы по соединяющим их шарнирам – устраняет две линейные связи;

в) введение (врезание) простого шарнира – устраняет одну угловую связь;

г) введение (врезание) ползуна – устраняет одну линейную связь;

д) удаление некоторых опорных связей;

е) сочетание вариантов п. «а, б, в, г, д».

Выбору варианта основной системы для раскрытия статической неопределимости методом сил (из множества возможных) следует уделить особое внимание, т.к. от этого, как это будет показано на примере, зависит объём вычислительной работы (при «ручном» расчёте), хотя окончательный результат и не зависит от выбора основной системы.

Неизвестные усилия в «лишних» связях обозначают X₁, X₂,··· X_i,···Х_n . ·

Условия эквивалентности заданной и эквивалентной систем заключаются в том, что перемещений в направлении устранённых связей как в заданной системе, так и в эквивалентной – нет.

(1.3)

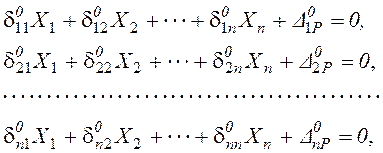Условия эквивалентности выражаются системой канонических уравнений (алгебраических), вытекающих из принципа суперпозиций (что применимо при соблюдении закона Гука и малых деформациях):

 

где  – коэффициенты системы уравнений – перемещения в основной системе в i-х направлениях от действия единичных сил ;

 – свободные (грузовые) члены системы уравнений – перемещения в основной системе в i-х направлениях от действия заданной нагрузки.

Заметим, что здесь и в дальнейшем при обозначении всех величин, относящихся к основной системе, вводим верхний индекс «0», а всё, что определяется в заданной системе, будем обозначать без этого индекса.

Для вычисления  и  необходимы эпюры изгибающих моментов в основной системе (учитываем только деформацию изгиба):

а) nтак называемых единичных эпюр  – от ;

б) грузовую эпюру  – от заданной нагрузки.

Перемещения  и  вычисляем «перемножением» соответствующих эпюр изгибающих моментов, что в символическом виде записываем:

.

Перемножение эпюр выполняем либо по правилу Верещагина, либо по готовым формулам, учитывая при этом изгибные жёсткости EI отдельных участков рамы.

Определение перемещений и правила перемножения эпюр отрабатывались в предыдущем задании «Перемещения в статически определимых балках и рамах».