Расчет статически неопределимых плоских рам методом сил: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика", страница 4

 – «площадь» эпюры поперечных сил от начала участка до сечения, где Q=0.

В нашем примере

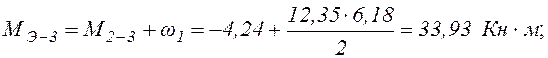
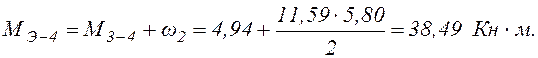
12). Cтроим эпюру продольных сил N.

Вырезаем узлы рамы 2, 3 и прикладываем в сечениях известные из эпюры Qпоперечные силы и неизвестные продольные силы (изгибающие моменты не показываем). Направления поперечных сил указываем в соответствии с принятым правилом знаков, а неизвестные продольные покажем «растягивающими», как это принято в расчёте ферм (рис. 13).

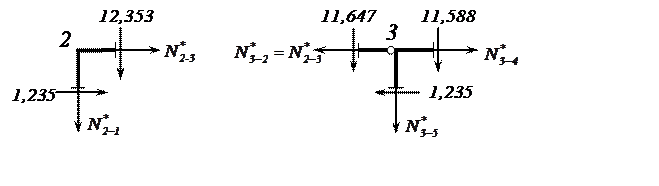
Рис. 13. Схемы узлов рамы для определения продольных сил

Из условий равновесия узла 2 получим:

;     

;      

Продольная сила на всех участках стойки 0-1-2 имеет постоянное значение, т.к. нет внешних нагрузок, направленных вдоль её оси.

Рассматривая равновесие узла 3, учтём, то , т.к. на участке 2-3 нет внешних нагрузок, направленных вдоль оси этого участка.

;         ,

Это значение соответствует отсутствию горизонтальной связи в сечении 4.

;         

Отрицательные значения продольных сил означают, что соответствующие стержни сжаты.

Эпюра N, построенная по этим значениям, представлена на рис. 14.

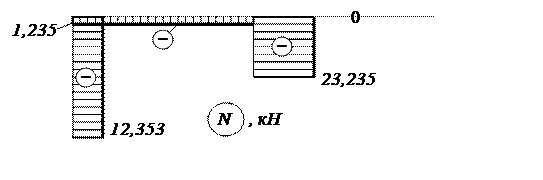
Рис. 14. Эпюра продольных сил N

13). Выполняем статическую проверку всех эпюр.

На рис. 15 показана расчётная схема рамы с отброшенными внешними связями и приложенными взамен им реакциями, значения и направления которых взяты с эпюр М, Q и N в соответствии с правилами знаков внутренних усилий.

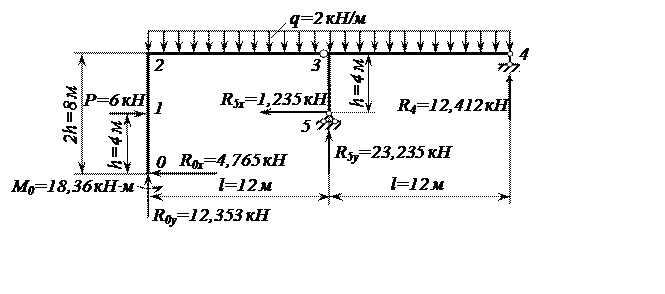
Рис. 15. Расчётная схема рамы с отброшенными опорными связями

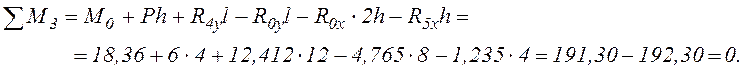
Здесь точка 3 взята произвольно (может быть взята и другая точка) из соображений, чтобы момент внешний нагрузки qотносительно этой точки был равен нулю.

Таким образом, все проверки подтверждают правильность раскрытия статической неопределимости рассматриваемой рамы.

В заключение покажем (без подробных комментариев), что решение задачи на этапе раскрытия статической неопределимости можно получить с меньшими затратами времени, если выбрать более удачный вариант основной системы, устранив две внутренние угловые связи в жёстких узлах 2 и 3 врезанием в эти узлы шарниров. Эквивалентная система, грузовая и единичные эпюры изгибающих моментов в этом случае имеет вид (рис. 16).

Система канонических уравнений внешне будет такой же, как и (2.1), но по содержанию (по физическому смыслу) – абсолютно другой.

.

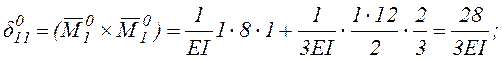
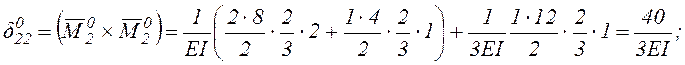
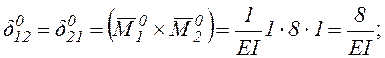
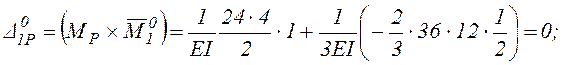
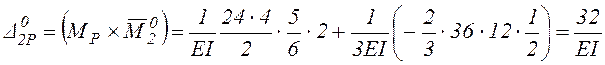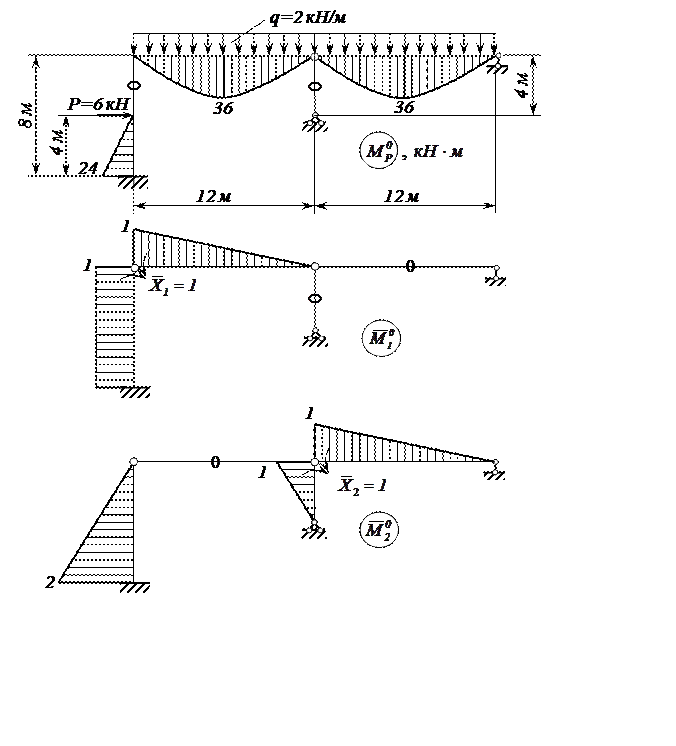
Рис. 16. Грузовое и единичные состояния основной системы

Решая систему уравнений

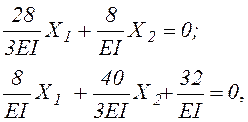
получим Х₁=4,24 кН·м; Х₂=4,94 кН·м.

Окончательную эпюру М_Р построим, как и ранее, суммируя «исправленные» единичные эпюры  и грузовую эпюру .

Предлагается эту процедуру выполнить самостоятельно и убедиться, что окончательная эпюра М_Р будет такой же, как и на рис. 9.

Упрощение решения здесь достигнуто за счёт более простого вида грузовой эпюры М_Р,т.к. основная система представлена в виде простых стержней, шарнирно сопряжённых между собой (простых шарнирно опёртых балок).

Подводя итоги, следует сказать о том, что для раскрытия статической неопределимости методом сил необходимо, кроме всего прочего, свободно владеть приёмами построения эпюр изгибающих моментов, методами определения перемещений в статически определимых рамах и балках. Эти вопросы рассматривались в первой части курса «Строительной механики» и отрабатывались в заданиях «Расчёт статически определимых балок и плоских рам», «Определение перемещений в статически определимых балках и рамах», поэтому построение эпюр изгибающих моментов грузового и единичных состояний и перемножение эпюр здесь не комментируются.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Дарков, А.В. Строительная механика: учебник для вузов / А.В. Дарков,

Н.Н. Шапошников. – 9-е изд., испр. – СПб. Лань, 2004. – 655 с.

2. Руководство к практическим занятиям по курсу строительной механики: Статика стержневых систем. Учеб. пособие для строит спец. вузов / Под общ. ред. Г.К. Клейна. – 4-е изд., перераб. и доп. – М.: Высш. школа, 1980, – 384 с.