Расчет статически неопределимых плоских рам методом сил: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика", страница 3

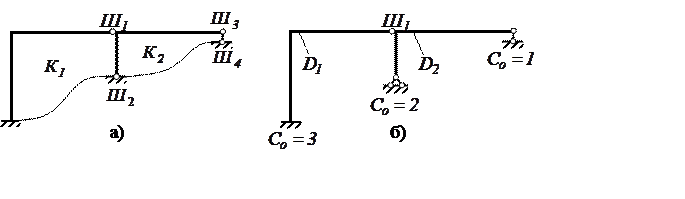
Рис. 3. Расчётные схемы рамы к определению степени

статической неопределимости

2). Выбираем основную систему.

Устраним две «лишние» связи, разъединив раму по простому шарниру в узле 3. В этом случае рама распадается на две статически определимые, геометрически неизменяемые рамы. В качестве неизвестных усилий будем определять вертикальную Х₁ и горизонтальную Х₂ составляющие внутреннего усилия (реакции) в шарнире.

Сразу же заметим, что это – не лучший вариант основной системы в смысле объёма вычислительной работы.

3). Представляем эквивалентную систему (рис. 4).

Рис. 4. Эквивалентная система

Предполагаемые направления Х₁ и Х₂ принимаем произвольно, учитывая при этом, что в левой и правой частях основной системы их направления взаимно противоположны, т.к. как это внутренние усилия в шарнире.

4). Записываем систему канонических уравнений в общем виде

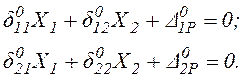                                                            (2.1)

5). Вычисляем коэффициенты  и свободные члены   как соответствующие перемещения единичных и грузового состояний основной системы.

С этой целью строим эпюры изгибающих моментов в основной системе и  от  и заданной нагрузки, соответственно (рис. 5).

Рис. 5. Эпюры изгибающих моментов в основной системе

единичных и грузового состояний

Напомним, что ординаты эпюр принято откладывать со стороны растянутых волокон, «0» на стержне обозначает отсутствие в нём изгибающего момента.

Вычисление  и   выполним, перемножая соответствующие эпюры по правилу Верещагина.

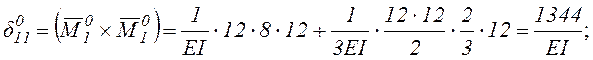
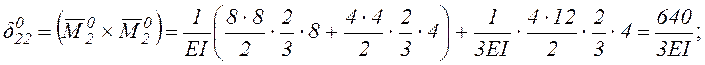
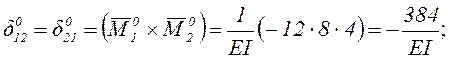
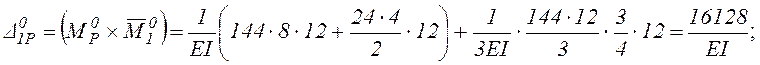
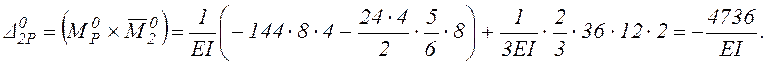
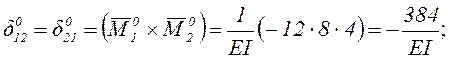
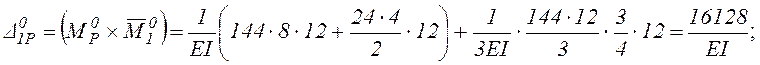
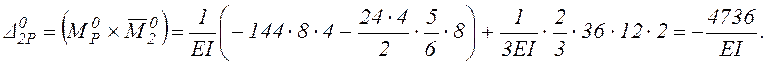
6). Проверим правильность предыдущих вычислений.

Для проверки построим суммарную единичную эпюру  (рис. 6).

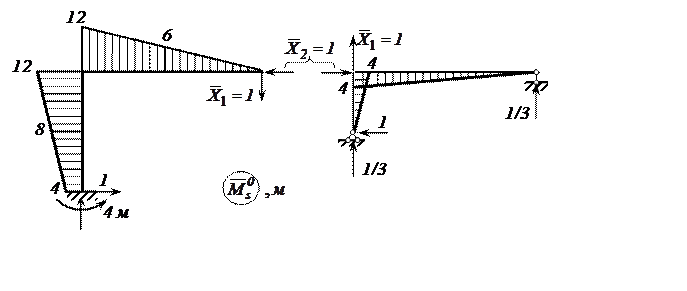
Рис. 6. Суммарное единичное состояние и эпюра

Перемножение эпюр при вычислении  и  выполним здесь, для разнообразия, по готовым формулам.

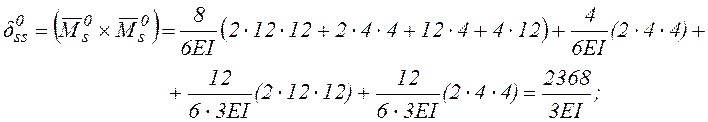
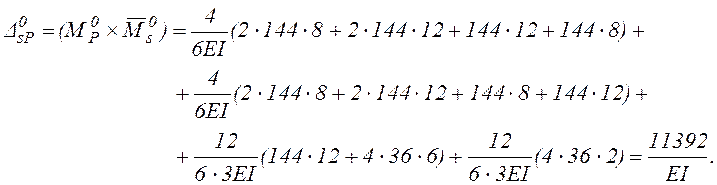
Проверим выполнение условий (1.4) и (1.5):

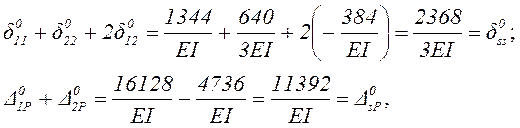
т.е.  и   вычислены правильно.

7). Подставляем найденные значения коэффициентов и свободных членов в систему канонических уравнений (2.1) и умножаем всё на EI.

1344Х₁ – 384Х₂ + 16128 = 0;

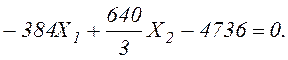
Решая систему уравнений, получим: Х₁=-11,647 кН; Х₂=1,235 кН.

8). Строим «исправленные» эпюры  и  (рис. 7).

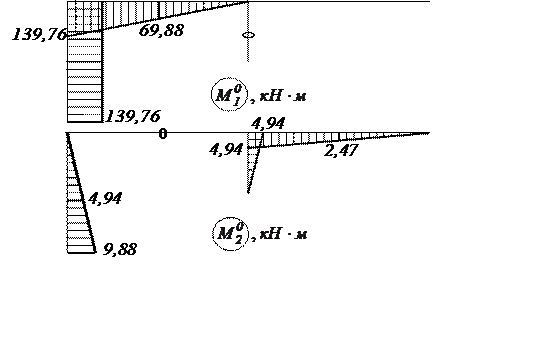
Рис. 7. Исправленные эпюры и

Заметим, что «исправление» эпюры  выполнено с учётом отрицательного значения Х₁.

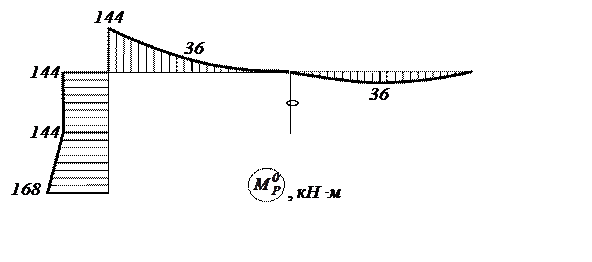
Рис. 8. Грузовая эпюра

9). Суммируя «исправленные» эпюры  и  с грузовой эпюрой   (рис. 8), получим окончательную эпюру изгибающих моментов М_Р (рис. 9).

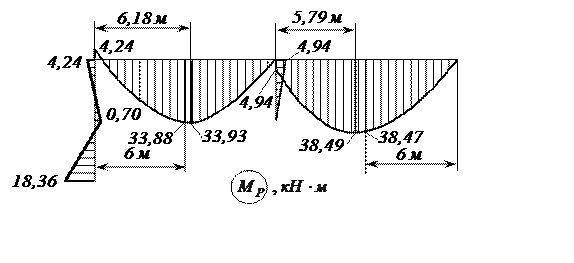
Рис. 9. Окончательная эпюра

10). Выполняем деформационную проверку полученного решения, перемножая окончательную эпюру  на суммарную единичную, построенную для другого – «нового» варианта основной системы (рис. 10, 11).

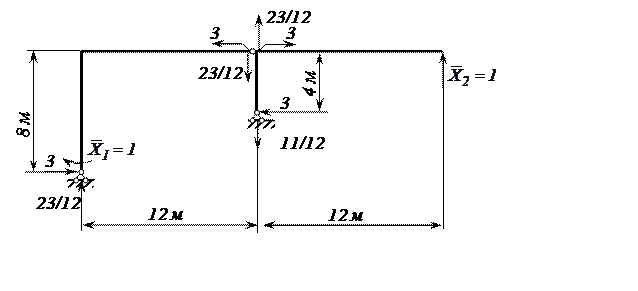
Рис. 10. Суммарное единичное состояние «нового» варианта

основной системы

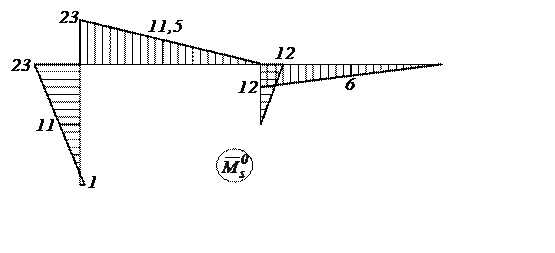
Рис. 11. Суммарная единичная эпюра

Используем готовые формулы перемножения эпюр.

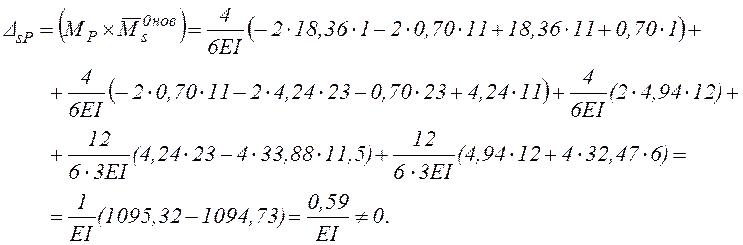
Примечание. Для оценки точности полученного решения при вычислении  отдельно «собраны» и разделены положительные и отрицательные значения.

Условие эквивалентности удовлетворяется с высокой точностью, т.к. относительная погрешность составляет

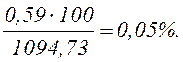
11). Убедившись в правильности раскрытия статической неопределимости, строим эпюру поперечных сил.

Значения поперечных сил на границах участков вычисляем по (1.7).

а). На участках 0-1, 1-2 и 3-5, где q=0, .

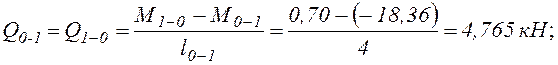
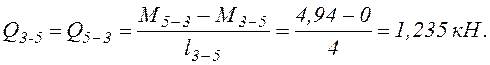
б). На участках 3-4 и 4-5 q=2 кН/м.

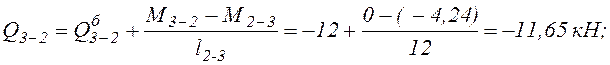
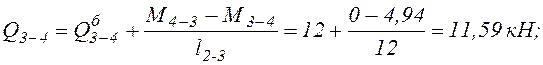
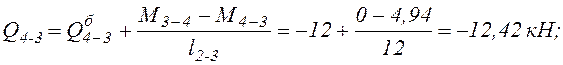
Эпюра поперечных сил Q, построенная по этим значениям, представлена на рис. 12.

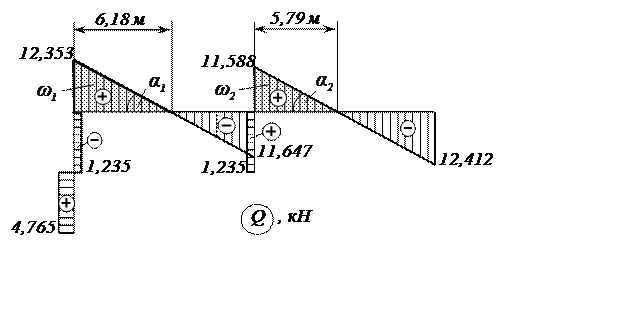
Рис. 12. Эпюра поперечных сил Q

На участках 2-3 и 3-4 имеются поперечные сечения, в которых Q=0, значит для этих сечений необходимо вычислить экстремальные значения изгибающих моментов. Положение этих сечений найдём, используя дифференциальную зависимость

,

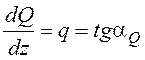где  – угол наклона эпюры Q.

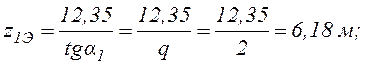
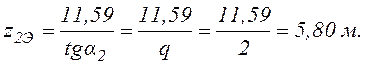
Экстремальные значения изгибающего момента вычислим с помощью интегрального соотношения между М и Q

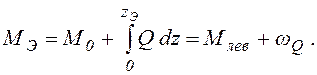
Здесь  – изгибающий момент в начале (в левом сечении) рассматриваемого участка;