Расчет статически неопределимых плоских рам методом сил: Методические указания к выполнению контрольной и расчётно-проектировочной работы по дисциплине "Строительная механика", страница 2

Рекомендуется выполнить проверку вычисления и , ибо при неправильном вычислении коэффициентов и свободных членов системы уравнений будет напрасно потрачено время на продолжение решение задачи.

Суть проверки в том, что суммарное перемещение  должно равняться сумме всех перемещений (коэффициентов) от единичных сил, т.е.

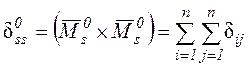,                                    (1.4)

а суммарное перемещение должно равняться сумме грузовых членов, т.е. 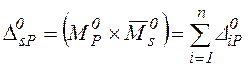.                                    (1.5)

Здесь  – суммарная эпюра изгибающих моментов от загружения основной системы всеми . Хотя эту эпюру можно построить, суммируя ранее построенные эпюры , но чтобы исключить возможные ошибки и свести тем самым на нет саму проверку, рекомендуется эпюру  строить независимо, рассматривая загружение основной системы всеми  одновременно.

Решение системы уравнений (1.3) может быть выполнено либо «вручную», например, по правилу Крамера, либо на ЭВМ. Если решение выполнятся «вручную», то следует убедиться в правильности решения, подставив полученные значения X_i в исходную систему уравнений.

Определив значения X_i– неизвестных в «лишних» связях, строят так называемую окончательную эпюру изгибающих моментов M_P в заданной статически неопределимой раме. Для этого «исправляем» единичные эпюры, умножая все их значения на соответствующие значения X_i (с учётом знака), и суммируем их с грузовой эпюрой M_P, т.е.

.

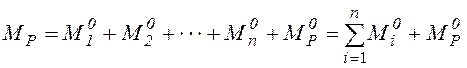Выполняется деформационная проверка полеченного решения – эпюры М_Р. Это проверка является основной и обязательной в методе сил, т.к. она при правильном раскрытии статической неопределимости подтверждает эквивалентность заданной и эквивалентной схем рамы при любом варианте основной системы. Поэтому для надёжности деформационной проверки рекомендуется использовать «новый» вариант основной системы и для него построить суммарную эпюру изгибающих моментов  от «новых» единичных сил .

Должно выполняться условие:

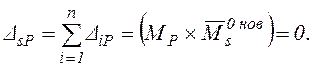                                   (1.6)

По эпюре изгибающих моментов М_Р строят эпюру поперечных сил Q и по ней – эпюру продольных сил N. При этом используются условия равновесия отдельных участков и узлов рамы.

Поперечные силы легко определить по формуле, полученной из условий равновесия отдельного участка рамы с известными значениями изгибающих моментов на левом и правом концах и внешней нагрузкой (рис. 1).

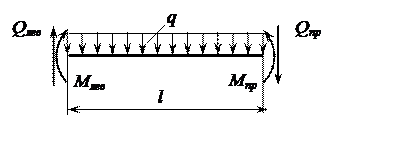
Рис. 1. Расчётная схема отдельного участка рамы

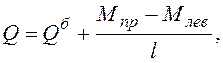                                          (1.7)

где  – так называемая балочная поперечная сила от внешней нагрузки;

М_пр – изгибающий момент на правом конце участка;

М_лев – изгибающий момент на левом конце участка;

l – длина участка.

Значения  необходимо брать с учётом знаков, учитывая при этом, что значения изгибающих моментов откладываются со стороны растянутых волокон (положительные – при растяжении нижних волокон).

Рама разбивается на участки, в пределах которых нагрузка q=0, либо q=const. В первом случае , во втором  со знаком в зависимости от направления q.

Не лишней будет и статическая проверка всех построенных эпюр. Для любой отсечённой части рамы или рамы в целом должны выполняться условия равновесия.

2. ПРИМЕР РАСЧЁТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ МЕТОДОМ СИЛ

Для рамы, представленной на рис. 2, требуется:

а) раскрыть статическую неопределимость, построить эпюру изгибающих моментов М_Р и выполнить деформационную проверку;

б) построить эпюры поперечных сил Q и продольных сил N;

в) выполнить статическую проверку эпюр.

Рис. 2. Расчётная схема рамы

Решение задачи выполняем по изложенной выше схеме.

1). Определяем степень статической неопределимости рамы.

По формуле (1.1) получим

.

Обозначения контуров и шарниров к формуле (1.1) приведены на рис. 3,а (шарнирно неподвижная опора в сечении 5 эквивалентно заменена шарниром).

Тот же результат получим и по формуле (1.2)

Обозначения опорных связей, шарниров и дисков к формуле (1.2) приведены на рис. 3,б.