Практикум по геомеханике, страница 3

Рисунок 1.1- Напряженное состояние элементарного объема

По закону о взаимности касательных напряжений, компоненты каса­тельных напряжений, расположенные симметрично относительно главной диагонали, составленной из компонентов нормальных напряжений, равны между собой:   

                                                          (1.3)

Такую симметричную квадратную матрицу называют тензором на­пряжений (1.2).

Кроме понятия напряжения в данной точке тела применяют также понятие деформация в данной точке, которое характеризует относительное изменение расстояния между точками тела в результате приложения внешних сил.

Механические процессы в породном массиве сопровождаются пере­мещениями его точек. Перемещение как векторную величину удобно раз- ложить на составляющие , которые являются проекцией перемеще­ния на координатные оси  и называются компонентами смещения рассматриваемой точки (рисунок 1.2).

Рисунок 2.1 - Деформированное состояние элементарного объема

Рассматривая в окрестности точки элементарный параллелепипед, имеем 6 компонентов деформации: три линейных и три угловых. Линей­ные деформации Е представляют относительные удлинения или укорочения ребер элементарного параллелепипеда (ε_x,ε_y,ε_z).

Угловые деформации или деформации сдвига представляют искаже­ния первоначально прямых углов ребрами элементарного параллелепипе­да. Угловые деформации выбывают только изменения формы. Их обозна­чают γ с двумя индексами: первый указывает координатную ось, параллельную ребру, поворот которого рассматривается, второй индекс - ось, параллельная  ребру,  в  направлении  которого  осуществляется  поворот

(1/2γ_xy,1/2γ_xz,1/2γ_yz).

Аналогично тензору напряжений компоненты деформированного со­стояния в рассматриваемой точке можно записать в виде симметричной матрицы:

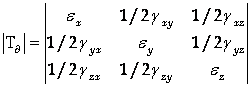                                                       (1.4)