Расчет характеристик системы передачи информации, структурная схема которой задана рисунком, страница 8

Λ₁ > Λ₀,

при выполнении этого неравенства регистрируется 1, не выполнении - 0.

  Алгоритм работы и структурная схема оптимального демодулятора  для заданного вида модуляции и способа обработки сигнала.

Для двоичной системы передачи сигналов правило оптимального некогерентного приема выражается в неравенством:

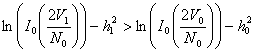
При выполнении данного условия считается, что пришёл сигнал s₁(t) (единица), в противном случае - сигнал s₀(t) (т.е. ноль).

Данный алгоритм и его реализация заметно упрощаются для двоичных систем с ОФМ (система с активной паузой). В этом случае алгоритм сводится к проверке одного неравенства:

.

где:

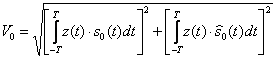
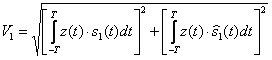
Поскольку при ОФМ информационный параметр сигнала определяется между двумя соседними элементами (на интервале от -T до T).

Для схемной реализации данный алгоритм также можно упростить. Для этого, сначала представим приходящий при ОФМ сигнал s(t) на двух тактовых интервалах в зависимости от символа, передаваемого n-м элементом:

, при передаче символа 0,

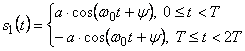, при передаче символа 1,

где - случайная начальная фаза, неизвестная при приеме, зависящая в частности, от символа передавшегося (n-2)-м элементом.

Далее, эти выражения для сигналов  и подставим в алгоритм приема и, после сокращения одинаковых слагаемых приведем алгоритм к виду:

, где:

; ;

;.

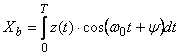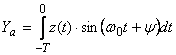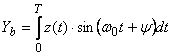В случае выполнения неравенства принимается символ 0, в противном случае символ 1.

Из того, что фаза  является хотя и случайной, но постоянной на интервале от –T до T, следует, что левая часть полученного алгоритма инвариантна к значению этой фазы.

Структурная схема оптимального некогерентного демодулятора для ОФМ (двоичной системы с активной паузой) на основе активных фильтров в соответствии с имеющимся алгоритмом имеет вид:

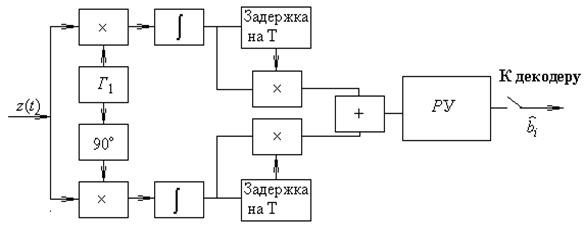
6.3Вероятность ошибки p оптимального некогерентного демодулятора.

Вероятность ошибки p оптимального некогерентного демодулятора при ОФМ определяется следующим выражением:

PОФМ=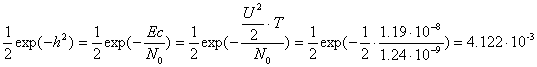

PОФМ=

6.4 Определить, как нужно изменить энергию сигнала (Е), чтобы при других видах модуляции и заданном способе приёма обеспечить вычисленное в п.3 значение вероятности ошибки р.

Так как при частотной модуляции вероятность ошибки определяется выражением:

,

а при амплитудной модуляции:

,

то, очевидно, что для обеспечения вычисленного в п.6.3 значения вероятности ошибки p необходимо при ЧМ увеличить энергию сигнала в 2 раза, при АМ – в 4 раза.

6.5  Считая выход демодулятора выходом двоичного симметричного канала связи, определить его пропускную способность: