Расчет характеристик системы передачи информации, структурная схема которой задана рисунком, страница 7

Где  m - коэффициент передачи канала равный 1.

Помехой является гауссовский шум, у которого спектральная плотность средней мощности постоянна и равна  в полосе частот канала Fk.

5.1 Расчёт минимально необходимой ширины полосы частот непрерывного канала

При выборе ширины полосы непрерывного канала необходимо учитывать, что любое расширение полосы пропускания увеличивает мощность помехи, а при  не только искажается форма сигнала, но и уменьшается энергия сигнала на выходе канала. Таким образом, минимально необходимая ширина полосы частот непрерывного канала:

= Гц

5.2 Расчёт мощности помехи n(t) на выходе канала.

Мощность помехи в полосе частот Fk = Fс :

5.3 Расчёт отношения Рс/Рn средней мощности сигнала  Рс к мощности помехи Рn.

Для двоичных равновероятных сигналов s₁(t) и s₀(t) их средняя мощность равна:

где Е₁ и Е₀ энергия соответственно сигналов s₁(t) и s₀(t):

, .

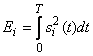Для ОФМ сигналов (система с активной паузой):

Тогда:

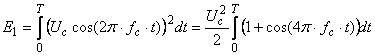
Примем . Тогда:

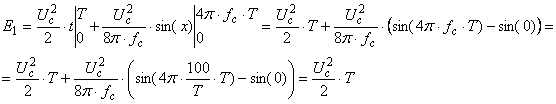
Очевидно, что: .

Средняя мощность сигнала:

 Вт.

Отношение Рс/Рn средней мощности сигнала  Рс к мощности помехи Рn:

5.4. Расчёт пропускной способности непрерывного канала в единицу времени С:

Пропускная способность непрерывного канала С определяется по формуле Шеннона:

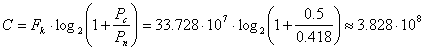бит/c.=382800кБод

5.5 Эффективность использования пропускной способности непрерывного канала :

Для оценки эффективности использования пропускной способности канала связи применяют коэффициент, равный отношению производительности источника Н’ к пропускной способности канала С’.

6.ДЕМОДУЛЯТОР

Демодулятор, оптимальный по критерию максимального правдоподобия в канале с аддитивной помехой, осуществляет некогерентную обработку принимаемого сигнала Z(t)=S(t)+n(t).

Для двоичной системы правило максимума правдоподобия сводится к проверке неравенства:   P(1)*w(z|1)>P(0)*w(z|0) .

Или рассматривают отношение правдоподобий Λ_{i j}:

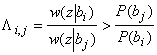
При равновероятной передаче cимволов  и рассмотрении дополнительной “шумовой” гипотезы можно записать отношение правдоподобий:

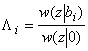
Тогда правило будет иметь вид:Λ_i > Λ_j при всех i ≠  j

А для двоичной системы правило сведется к проверке: