Расчет характеристик системы передачи информации, структурная схема которой задана рисунком, страница 4

2.3 Мощность шума квантования P_шк  и ее относительная величина при сравнении с мощностью переменной составляющей непрерывного сообщения.

Закон распределения имеет вид, аналогичный закону распределения процесса а(t). То есть можно записать:

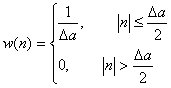
P_шк=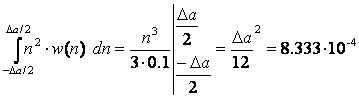 B².= 83,3мВ

            Определим относительную величину мощности шума квантования по сравнению с мощностью переменной составляющей

2.4 Минимальное число двоичных разрядов k, требуемое для записи в виде двоичного числа любого номера из L номеров уровней квантования:

 бит

2.5 k- разрядное двоичное число, соответствующее заданному номеру j уровня квантования a_j:

2.6 Временная диаграмма отклика АЦП на уровень с заданным номером j (в виде последовательности биполярных импульсов):

 

2.7 Энтропия Н и производительность Н′ при условии, что все отсчеты непрерывного сообщения взаимнонезависимы

 

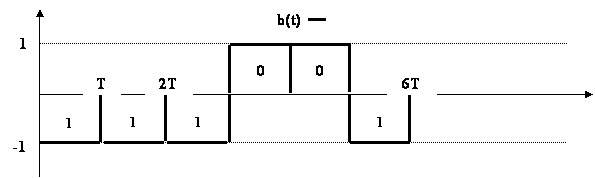
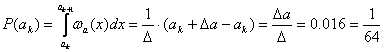Так как все отсчеты взаимонезависимы, то энтропия АЦП вычисляется по формуле

 

Производительность АЦП рассчитывается по следующей формуле:

3.кодер

Кодер выполняет систематическое кодирование с одной проверкой на чётность, образуя код (n,k). При этом символы двоичного числа, образованного номером уровня, становятся информационными символами кодового слова. На выходе кодера последовательность кодовых символов bкаждого n-разрядного кодового слова b преобразуется в импульсную последовательность b(t) по правилу, приведённому в пункте 6 предыдущего раздела. Длительность импульсной последовательности, соответствующей каждому кодовому слову, одинакова и равна . Сигнал b(t) на выходе кодера представляет собой случайный синхронный телеграфный сигнал.

3.1 Расчёт минимального значения разрядности кода (k)  необходимого для   примитивного кодирования всех L уровней квантованного сообщения a(ti).

Из теории кодирования известно, что канальным (помехоустойчивым) кодом называется множество из М различных последовательностей x₁, x₂ , x₃,…,x_M одинаковой длины n, каждая позиция которых может принимать любое из m значений входного алфавита Х если  M≤mⁿ. Причем при выполнении равенства код является примитивным (безизбыточным), а разрядность кода минимальна. Тогда, в нашем случае, минимальное значение разрядности кода k определим из выражения (учитывая, что - основание кода в нашем случае, а - число возможных последовательностей):