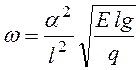 с-1, (7.9)
с-1, (7.9)
где a — величина, зависящая от условий защемления на опорах, принимаемая для трубопроводов с шарнирными опорами a = 3,14, а для трубопроводов с защемленными опорами a = 4,76; Е — модуль упругости, кг/см2; g— ускорение силы тяжести, см/с2; I — момент инерции поперечного сечения, см4; l— длина пролета между опорами трубопровода, м; q— собственный вес трубопровода, кг.
Из формулы (7.9) вытекает, что частота собственных колебаний обратно пропорциональна квадрату расстояний между порами.
При определении частоты собственных колебаний труб и балок наибольшие затруднения вызывает нахождение коэффициента a. Покажем методику определения a для некоторых схем расположения трубопроводов.
Значения коэффициентов a для многопролетных трубопроводов (рис. 7.5) с равными пролетами можно принимать одинаковыми независимо от условий крепления на крайних опорах. Так, для основной частоты рекомендуется принимать a1 = 3,14; для первой гармоники a2 = 6,28.
Коэффициент a1 для определения основной частоты одноконсольной балки с двумя опорами находят в зависимости от величины отношения l2/l1 (рис. 7.6).
|
a1 |
l2/l1 |
a1 |
l2/l1 |
|
1,5059 |
1 |
3,1175 |
1/6 |
|
1,9017 |
3/1 |
3,1265 |
1/7 |
|
2,5189 |
1/2 |
3,1315 |
1/8 |
|
2,9401 |
1/3 |
3,1345 |
1/9 |
|
3,0588 |
1/1 |
3,1364 |
1/10 |
|
3,0997 |
1/5 |
 |

При l2/l1< 1/2 значение a1 можно определить по формуле
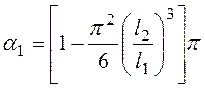 . (7.10)
. (7.10)
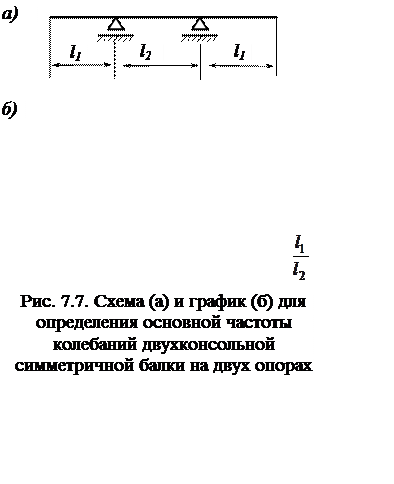
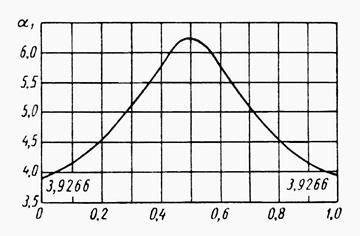
Коэффициент a1 для двухконсольной балки с двумя опорами (рис. 7.7, а) определяется по графику на рис. 7.7, б. Кроме равномерно распределенной нагрузки (собственный вес, изоляция и т.п.) отдельные участки балок и труб могут нести сосредоточенные нагрузки.
Основная частота собственных колебаний для некоторых балок с равномерно распределенной и сосредоточенной нагрузками определяется по следующим формулам:
а) консоль с сосредоточенной нагрузкой на конце
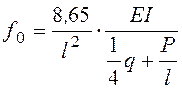 ; (7.11)
; (7.11)
б) однопролетная балка с шарнирными опорами и грузом посередине
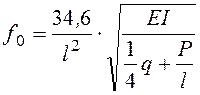 ; (7.12)
; (7.12)
в) однопролетная балка с заделанными опорами и грузом посередине
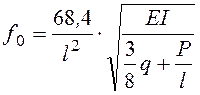 . (7.13)
. (7.13)
Для окончательной оценки характера колебаний трубопровода необходимо сравнение фактически замеренных частот собственных колебаний с теми же частотами, вычисленными по формулам (трубопровод рассматривается как неразрезанная балка).
Точный расчет такой системы с большим числом пролетов разной величины и наличием искривлений трубопровода является весьма сложным. Поскольку и первую очередь необходимо сравнение порядка экспериментально полученных и вычисленных величин, то можно ограничиться вычислением частот для интересующих нас расстояний между опорами как для однопролетных балок (при полной заделке и шарнирном опирании).
|
||||
 |
||||
Модуль упругости стали Е = 2 100 000 кг/см2, ускорение силы тяжести g = 981 см/с2.
Момент инерции поперечного сечения трубопровода
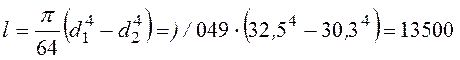 см4.
см4.
Погонная нагрузка, равномерно распределенная по длине (собственный вес),
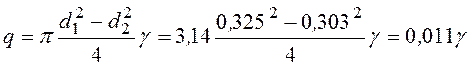 ,
,
где g - объемный вес металла, т/м3 (g = 7,85 т/м3).
Поэтому
q = 0,011×7,85 = 0,086 т/пог. м = 0,86 кг/см.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.