Строительство и архитектура \ Изыскания и проектирование железных дорог

Определение возможности применения железобетонных шпал типа IllC-ly при обращении четырехосных грузовых вагонов с повышенными осевыми нагрузками

Страницы работы

6 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

1.13. ПРИМЕР РАСЧЕТА ЖЕЛЕЗОБЕТОННОЙ ШПАЛЫ

Требуется определить возможность применения железобетонных шпал типа IllC-lyпри обращении четырехосных грузовых вагонов с повышенными осевыми нмфузками до 230 кН (23 тс) со скоростью 80 км/ч в кривых.

1. Определениевертикальныхигоризонтальныхсил, действующихнашпалу

1'асчетные характеристики вагона: Я_Ст = П5кН; d—0,95м; q=\\кН; н, 2 кН/мм; /i = 1,80 м; a_t= 0,67 мм.

Расчетные характеристики пути: рельсы Р50 с приведенным износом 6 мм, v 1813 см⁴ = 1,813- 10~⁵м⁴, /_г = 377 см< = 0,377-10~⁵ м⁴, р = 1; число шпал • |.| I км в кривой 2000; / = 0,50 м; балласт щебеночный, f= I; рельсовое скрепле-MII¹ ища КБ с упругими прокладками толщиной 7 мм.

По табл. 3.1и= 167 МПа. По табл. 3.2 «₂ = 72 МПа; н_ф = 329 кН/рад.

A i V

-5 ⁼¹'⁸² ^М~^!-

По формуле (3.10) 1/

4-2,Ы0⁵-1,813-10~⁵

133

По формуле (3.6) •^гтах= Ю+ 1б-Ю~⁴-80² = 20,24 мм.

По формуле (3.3) Р_р = 20,24-2 =40,48 кН.

По формуле (3.2) Р_ср = 115 + 0,75.40,48 = 145,36 кН.

По формуле (3.8) 5_р =0,08-40,48 = 3,24 кН.

По формуле (3.9)

• 145,36-80 = 9,93 кН.

S_Iin = 0,538-10-⁴-l-0,50|/ j-gg-По формуле (3.1Г)

²^11

= 1,51 кН.

0,2Ы0~⁵ • 167-80

____

^ннк ~ 0,95² Уо,1-1,82-167—0,0326-1,82²-11

По формуле (3.12')

0,3-167-0,67
5„„к = —f^2--- = 18.44 кН.

По формуле (3.13) 5_нер = 0,167-145,36 = 24,28 кН.

По таблицам [17] для Ы_х= 1,82-1,80 = 3,28 находится т\ =—0,0424. Эквивалентная нагрузка, учитывающая влияние смежной оси вагонной тележки, ^Я_ср =—0,0424-145,36 = —6,16 кН. По формуле (3.1)

Р_дан = 145,36+2,5 УЗ,24²+9,952+24,28²+0,95-1,512+0,05-18,44² — 6,16 = = 139,20+2,5-26,79 = 206,18 кН.

Для четырехосного грузового вагона при ^й_нп = 0,7 м/с²; Z=31,5+26-0,7= = 49,70 кН; Н= 54+25-0,7 = 71,50 кН. ; По формуле (3.15')

(2_р)_ди„ = 49,7 (1+0,0024-80) = 59,24 кН; Я_днн = 71,5 (1+0,003-80)=88,66 кН. По формуле (3.14')

По формуле (3.14) Р_лин = 206,18 + 17,59 = 223,77 кН.

По формуле (3.17)

= 101,82 кН.

1,82-0,50-223,77
~ 2

По формуле (3.18')

•м

4-2,Ы0⁵-0,377-10~⁵По формуле (3.18)

2,18-0,50-88,66
"т^-------- §---- =48,32 кН.

По формуле (3.22) •И_щ =48,32 (0,102 + 0,026) = 6,18 кН-м.

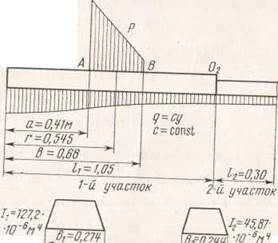
Схема сил и моментов, действующих на шпалу, представлена нарис. 3.10. По формуле (3.21)

•• = 0,132 + 2 (0,102 + 0,026) ctg 60° = 0,27 м,

где 0,132 — ширина подошвы рельса Р50; h'_m = 0,102 м; h_a—0,014 + 0,005 + |-"0,007 = 0,026 м — суммарная толщина подкладки типа КБ, прокладки под рельсом и прокладки под подкладкой.

По формулам (3.23) и (3.23')

^р ~ 0,27+ 0,272

или после преобразования

Рис. 3.10. Схема сил я моментов, действующих на шпалу ШС-ly в кривой

р= 3,7037Р_ш + 80,3045М_ш ;

Др=609,66Л*_ш

2. Определениеудельныхизгиба- д ющихмоментов, поперечныхсили ' прогибов (давленийнабалласт)

Расчетная схема шпалы показана на рис. 3.11. Расчет проводится при различных значениях коэффициента постели (от 8 до400-10⁴ кЙ/м³), после чего во внимание принимаются наиболее невыгодные случаи. Примем - = 13-10⁴ кН/м³.

-•127,2- 10~⁶м* 325

/.•-чокпп дГп ^{^М-^ниже ^п- 3), ^------- ч р^1^ц

На первом, подрельсовом, участке •мпалы: *i=0,274 м; 1_Х= 12 720 см*= • ¹^OV ° ¹"-^fi ' (см. ниже п. 3),

134

135

По формуле (3.24)

-1

ГЙ=1.2м

/и, = 1/

Y0,274-13-Ю⁴

4.3,25-10М27,2-10

Л_г = 0,5824, В_г= 1,1545,

Для конца первого, подрельсового, участка: z= 1,05-1,2 = 1,26; г— а=• = 1,2(1,05—0,41) = 0,768; г —р = 1,2(1,05—0,68) = 0,444. Для этих аргументов по таблицам [18] находим:

__а = 0,9421, Л_г__р = 0,9936;

__я =0,7591, В_г„_р = 0,4434;

С_г =0,7716, С_г__а = 0,2938, С_г__р = 0,0985;

D₃= 0,3294, £>_г__ч = 0,07536, D_z__? = 0,01462.

По формулам (3.33)—(3.36)

р Д/>

Afi = 0,7716S₀ + O,3294jVo — утр- (0,2938—0,0985) — -y-gr 0,27-0,0985 +

+ "^-(0,07536—0,01462);

Qi= l,2(l,1545S₀ + 0,7716A^ro)— 1^(0,7591—0,4434) —j-j 0,27-0,4434-

Для середины шпалы Q_x = 0 и Ф_Л = 0. Используем уравнения (3.38) и (3.40):

—4-1,52-0,01582iWi + 0.9928Q, +0,8909 р^ К, +0,8909 р^^Ф, = 0;

t—4-1,52³-0,4554,М₁ —4-1,522-0,1039Qi —0,8909-1,52-4-0,01582Г; + |-О,8909-0,9928Ф1 =0.

Подставив в эти уравнения выражения для Mi, Qi, У\, Ф1 и решив эти уравнения относительно 5₀ и Л^о, получим:

So = 0,168056р — 0,019691Др; ' ^о = —0,013313р —0,002241Др.

Определим удельные значения изгибающих моментов, поперечных сил и проги-(давлений на балласт) в наиболее характерных точках шпалы. КонецшпалыМ= 0, Q = 0:

:0,006794р-

_________ (0,168056р— 0,019691 Др) 1,2²-1000

^Уо⁼ К~с⁼0,274-130 000

0,000796Др, мм. Введем вместо ри Др их выражения через Р_ши М_ш

= 0,025162Я_ш

v₀ = 0,006794 (3,7037Р_ш + 80,3045М_ш) — 0,000796-609, + 0,060297М_ш_-

Др

(0,2938—0,0985);

Ki = l,2²(0,5824S₀+ 1,1545iV₀) —p (0,9421— 0,9936)— Др-0,27-0,9936 +

+ 4т (0,7591—0,4434);

Ф1 = 1,2³(—4-0,3294S₀ + 0,5824Л^г₀) +4-1,2p (0,07536—0,01462) +

+ 4-1,2-0,27-0,01462- Др + Др (0,9421—0,9936).

После определения числовых коэффициентов уравнения примут вид; Mi= 0,7716S₀ +0,3294Л^о — 0,135625р + 0,016682Др; Qi= 1,3854S₀ +0,9259ЛГ₀ —0,263083/?+ 0,035860 Др;

-l,6625JV₀ + 0,051500/> —0,005189Др;

- 1,0064ЛГ₀ +0,291552р —0,032553Др. На втором, среднем, участке шпалы Ь₂ = 0,245 м, /₂ = 45,87-10~⁵ м*